基本定義
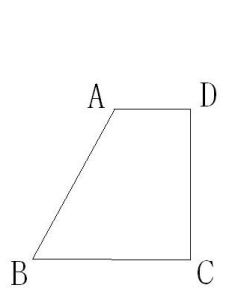
 直角梯形
直角梯形面積公式
S=(上底+下底)×高÷2梯形是上下兩條邊平行的四邊形狀,你按照一個對角線可以把它分成兩個高相同的三角形,三角形面積公式是“底乘以高除以2”,所以梯形就是:“上底乘以高除以2”+“下底乘以高除以2”=“上底加下底乘以高除以2”
另一個公式:“中位線×高”,其中“中位線”是(上底+下底)除以2。
具有特徵
在直角梯形ABCD中,AD//BC,∠B=90°,則∠A=90°,∠C+∠D=180°。重要性質:
直角梯形斜腰的中點到直角腰的二端點距離相
| 八邊形 | ▪八面體 | ▪百分比 | ▪百分點 |
| ▪百分位數 | ▪半徑 | ▪半球 | ▪半圓 |
| ▪被乘數 | ▪被除數 | ▪被加數 | ▪被減數 |
| ▪比 | ▪比例 | ▪邊 | ▪變數 |
| ▪標準差 | ▪表面積 | ▪並集 | ▪補集 |
| ▪不等邊三角形 | ▪不等式 | ▪不定積分 | ▪差 |
| ▪長 | ▪常量 | ▪乘 | ▪乘方 |
| ▪乘數 | ▪除 | ▪除數 | ▪垂心 |
| ▪次方 | ▪次方根 | ▪大於 | ▪大於等於 |
| ▪代數 | ▪單調性 | ▪單項式 | ▪導數 |
| ▪等邊三角形 | ▪等式方程式 | ▪等腰三角形 | ▪等腰梯形 |
| ▪等於 | ▪底 | ▪底面 | ▪點 |
| ▪定積分 | ▪定理 | ▪定義域 | ▪對數 |
| ▪鈍角 | ▪鈍角三角形 | ▪多邊形 | ▪多面體 |
| ▪二次方程 | ▪多項式 | ▪二次方根平方根 | ▪二次方平方 |
| ▪二進制 | ▪二十面體 | ▪反餘割 | ▪反餘切 |
| ▪反餘弦 | ▪反正割 | ▪反正切 | ▪反正弦 |
| ▪方差 | ▪非常態分配 | ▪分布 | ▪分母 |
| ▪分數 | ▪分子 | ▪負 | ▪複數 |