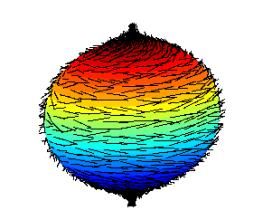
定理描述
 毛球定理
毛球定理實際上,根據龐加萊·霍普夫定理,三維空間中的向量場的零點處的指數和為2,即二維球面的歐拉示性數,因此零點必然存在。對於二維環面,其歐拉特徵數為0,因此“長滿毛的甜甜圈”是有可能被“撫平”的。推廣來說,對於任意的正則的偶數維緊流形,若其歐拉示性數不為0,則其上的連續的切向量場必然存在零點。
定理與氣鏇
 毛球定理
毛球定理這樣看來,一個完全沒有風的點(空氣靜止)對應著向量場的一個零點。事實上,就物理上來說,空氣是不可能在某一個區域處處絕對靜止的,因為空氣總在運動。但毛球定理說明零點存在,因此必然有空氣靜止的點,並且是孤立點。
一個物理學上的解釋是這些零點對應著氣鏇或反氣鏇的中心(風眼)。在這樣的零點附近,風的分布成螺鏇形,但永遠不會從水平吹入中心或從其中吹出(只能上升或下降)。由毛球定理可以得出,地球表面永遠存在氣鏇和風眼,在風眼處風平浪靜,但四周都有風環繞。
數學定理
A-F
| ▪15定理 | ▪2π定理 | ▪Sun-Ni定理 | ▪Vizing定理 |
| ▪阿貝爾定理 | ▪阿貝爾二項式定理 | ▪阿貝爾-魯菲尼定理 | ▪阿貝爾曲線定理 |
| ▪阿達馬三圓定理 | ▪阿蒂亞-辛格指標定理 | ▪阿爾澤拉-阿斯科利定理 | ▪阿基米德原理 |
| ▪阿基米德中點定理 | ▪埃爾布朗定理 | ▪艾森斯坦定理 | ▪安達爾定理 |
| ▪奧爾定理 | ▪巴拿赫不動點定理 | ▪巴拿赫-塔斯基悖論 | ▪貝爾綱定理 |
| ▪貝亞蒂定理 | ▪貝葉斯定理 | ▪貝祖定理 | ▪本迪克森-杜拉克定理 |
| ▪本原元定理 | ▪閉圖像定理 | ▪波爾查諾-魏爾斯特拉斯定理 | ▪伯恩斯坦定理 |
| ▪伯特蘭-切比雪夫定理 | ▪博蘇克-烏拉姆定理 | ▪博特周期性定理 | ▪不動點定理 |
| ▪布爾素理想定理 | ▪布朗定理 | ▪布勞威爾不動點定理 | ▪布列安桑定理 |
| ▪採樣定理 | ▪陳氏定理 | ▪垂徑定理 | ▪達布中值定理 |
| ▪大數定律 | ▪代數基本定理 | ▪單調收斂定理 | ▪單值化定理 |
| ▪等周定理 | ▪狄利克雷定理 | ▪迪尼定理 | ▪笛卡兒定理 |
| ▪笛卡兒符號法則 | ▪笛沙格定理 | ▪棣莫弗定理 | ▪棣莫弗-拉普拉斯定理 |
| ▪多項式定理 | ▪多項式餘數定理 | ▪二次互反律 | ▪二項式定理 |
| ▪法圖引理 | ▪法伊特-湯普森定理 | ▪凡·奧貝爾定理 | ▪反函式定理 |
| ▪范德瓦爾登定理 | ▪費馬大定理 | ▪費馬多邊形數定理 | ▪費馬平方和定理 |
| ▪費馬小定理 | ▪芬斯勒-哈德維格爾定理 | ▪弗羅貝尼烏斯定理 | ▪輻角原理 |