定義
正規擴張的定義不止一種,以下三個準則都可以刻畫正規擴張,是三個等價的定義。域擴張L/K是正規擴張若且唯若它滿足以下三個等價條件中任意一個:
1.L是多項式環K[X]中的某一族多項式的分裂域。
2.設K是一個包含了L的K的代數閉包。對於L在K上的每一個嵌入σ,只要它限制在K上的部分是平凡的(即為恆等映射:σ(x)=x),那么就有σ(L) =L。換句話說,L在K上的每一個K-嵌入σ都是一個L上的K-自同構。
3.任意一個K[X]上的不可約多項式,只要它在L中有一個根,那么就可以在L[X]分解成一次因式的乘積(或者說全部的根都在L中)。
例子
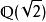 正規擴張
正規擴張 正規擴張
正規擴張 正規擴張
正規擴張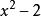 正規擴張
正規擴張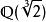 正規擴張
正規擴張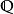 正規擴張
正規擴張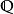 正規擴張
正規擴張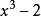 正規擴張
正規擴張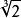 正規擴張
正規擴張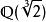 正規擴張
正規擴張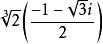 正規擴張
正規擴張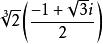 正規擴張
正規擴張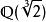 正規擴張
正規擴張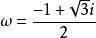 正規擴張
正規擴張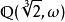 正規擴張
正規擴張是 的一個正規擴張,因為它是 上的多項式 的分裂域。然而, 並不是 的一個正規擴張,因為 上的不可約多項式 有一個根: 在 裡面,但它的另外兩個根: 和 都是複數,不在 裡面。只有在加入了三次單位根: 後的擴域 才是一個正規擴張。
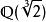 正規擴張
正規擴張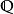 正規擴張
正規擴張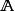 正規擴張
正規擴張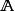 正規擴張
正規擴張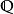 正規擴張
正規擴張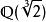 正規擴張
正規擴張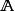 正規擴張
正規擴張也可以用正規擴張的第二個定義來證明 不是 的正規擴張。設域 是由所有復代數數生成的擴域,則 是 的一個代數閉包,並且 在 裡面。另一方面,
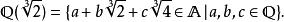 正規擴張
正規擴張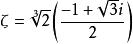 正規擴張
正規擴張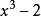 正規擴張
正規擴張並且,如果記 是 的復根之一,那么映射:
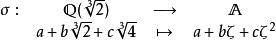 正規擴張
正規擴張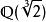 正規擴張
正規擴張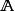 正規擴張
正規擴張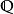 正規擴張
正規擴張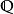 正規擴張
正規擴張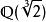 正規擴張
正規擴張是 在 上的一個嵌入,並且它限制在 上的部分是平凡的(將 中元素映射到自己)。但是σ並不是 上的自同構。
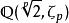 正規擴張
正規擴張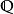 正規擴張
正規擴張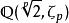 正規擴張
正規擴張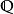 正規擴張
正規擴張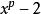 正規擴張
正規擴張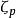 正規擴張
正規擴張更一般地,對每一個素數p,域擴張 都是 的一個正規擴張,擴張的次數是p(p-1)。 是 上的多項式 的分裂域。其中的 是任意一個複數p次單位根。
性質
設有域擴張L/K,那么:
1) 如果L是K的正規擴張,並且F是一個子擴張(也就是說有擴張K⊂F⊂L)那么L也是F的正規擴張。
2) 如果L的子域E和F都是K的正規擴張,那么兩者的複合擴張EF(指L的子域中同時包含E和F的最小者)以及兩者的交E∩F也都是K的正規擴張。
正規閉包
設有域擴張L/K,那么總存在域擴張M/L,使得M/K是正規擴張。在同構意義上,最小的這樣的擴張是唯一。即是說,其他的域擴張N/L如果使得N/K是正規擴張,那么總存在N/L的子擴張M'/L,使得M'同構於M。這個唯一的“最小”正規擴張M/L稱為域擴張L/K的 正規閉包。
如果L/K是有限擴張,那么它的正規閉包M/L也是有限擴張(因此M/K也是有限擴張)。
