群擴張

在抽象代數中，設Q為群，若存在群G，N，及群的正合序列，則稱群G為Q的群擴張，或稱Q對N的擴張。

簡介

在抽象代數中，設Q為群，若存在群G，N及群的正合序列

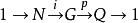群擴張

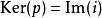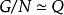群擴張

群擴張

（換言之，i是單射、p是滿射，且 ；是故可視N為G的正規子群， 。）則稱群G為Q的 群擴張，或稱Q對N的擴張。

由短正合序列的同構關係，可以定義群擴張的 等價類。若某個群擴張等價於

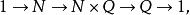群擴張

則稱此擴張為 平凡擴張。當N落在G的中心時，稱之為 中心擴張。

分類

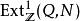群擴張

一般的群擴張不易分類。若限定G為阿貝爾群，則Q對N的擴張等價類一一對應於 （參見條目Ext函子）。

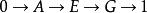群擴張

群擴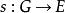張

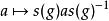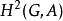群擴張

群擴張

另一方面，若在群擴張 中，A為阿貝爾群，可任取一截面 （s 不一定是群同態），群G以共軛方式 在A上作用。這類擴張的等價類由群上同調 分類，並具有自然的群結構。最常見的例子是中心擴張。

李代數的擴張

利用同樣作法，也可以定義李代數的擴張。此即李代數的正合序列

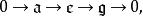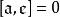群擴張

群擴張

若 ，稱之為中心擴張。