正則變換
設某系統存在著一組廣義坐標q1,q2,…,qN和廣義動量p1,p2,…,pN,而變數變換式為: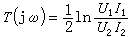
,
而且使系統原來的正則方程,
(i=1,2,…,N)變換到以K為哈密頓函式的另一組正則方程,(i=1,2,…,N) (2)
則式(1)稱為正則變換。式(2)中的K(Q,P,t)是新哈密頓函式。根據正則方程與廣義哈密頓原理的等價性,上述要求也可表述為:
(3)
如果上式同時成立,其被積函式應滿足(4)
式中F稱為正則變換的“母函式”。由於4N個新老正則變數之間有2N個變換關係式相聯繫,可在其中選出2N個變數作為獨立變數。 假定某類正則變換可以選擇(q,Q)這2N個變數作為獨立變數,則F可表達為(q,Q,t)的函式,並記為F1。於是有:(5)
而
將上式代入(5)中,比較係數得:,(6)
式中F1稱為“第一類的母函式”,可以按要求適當選定。F1選定後,可自式(6)的第一式解出Q,再自第二式算出P,K可由式(6)的末一式求得。這樣求得的Q,P,K一定適合正則方程:。
在4N個新老正則變數中,如果對2N個獨立變數的取法不同,則母函式的形式也不同。常用的母函式有F1(q,Q,t),F2(q,P,t),F3(p,Q,t),F4(p,P,t)。它們之間的關係可寫為: 施行正則變換的目的是將正則方程變換成較易求解的方程。如選擇正則變換,使變換後的新哈密頓函式,則這種變換後的新廣義坐標全部成為可遺坐標。由式(2)得:,
故Qi=αi,Pi=βi, 式中αi,βi分別為積分常數。假定上述正則變換的母函式為F1,根據式(6)的末一式,應該有:
。(7)
將F1寫成S(q,Q,t),再把式(6)中的第一式代入式(7)中便得到: 這就是著名的哈密頓-雅可比方程,通過它的全積分可以找到滿足上述要求的正則變換。正則變換的研究在天體力學中有廣泛的套用。
