定義
如果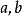 是非零整數,而整數
是非零整數,而整數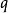 同時是
同時是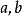 的因數,我們便把
的因數,我們便把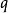 叫做
叫做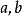 的公因數。
的公因數。
顯然,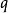 的絕對值必然不大於
的絕對值必然不大於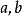 的絕對值的最小者,即
的絕對值的最小者,即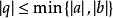
上式表明,兩個非零整數的公因數必只有有限多個,於是,其中一定存在一個最大的。我們把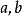 的所有公因數中最大的一個公因數
的所有公因數中最大的一個公因數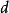 ,叫做
,叫做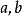 的最大公因數,記作
的最大公因數,記作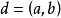 。
。
最大公因數
分解素因數法
求幾個整數的最大公因數,是先把這些數分別分解素因數,並寫成乘方形式,然後在各個共有的素因數里,取出指數最小的乘方相乘即得最大公因數。
例:求1008,1260,882和1134的最大公因數。
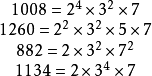
所以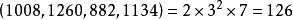 。
。
輾轉相除法
用輾轉相除法求兩個非零整數的最大公因數的具體步驟如下:(不妨設![]() 均為正整數,且
均為正整數,且![]() )
)
先用![]() 除
除![]() ,得到正整數
,得到正整數![]() ,使
,使
若![]() ,則由
,則由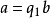 知
知![]() 與
與![]() 的最大公因數是
的最大公因數是![]() 。若
。若![]() ,由
,由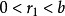 ,可再以
,可再以![]() 除
除![]() ,於是又可得到正整數
,於是又可得到正整數![]() 和非負整數
和非負整數![]() ,使
,使
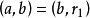 。
。當![]() 時,
時,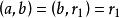 ;若
;若![]() ,則
,則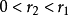 ,再以
,再以![]() 除
除![]() 得正整數
得正整數![]() 和非負整數
和非負整數![]() ,使得
,使得
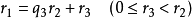
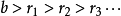 ,且各
,且各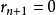 ,但
,但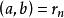 。
。這樣就通過輾轉相除得到了 ![]() 與
與![]() 的最大公因數。
的最大公因數。
性質
①如果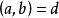 ,則存在整數
,則存在整數![]() ,使
,使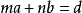 。
。
②如果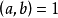 ,則我們稱
,則我們稱![]() 與
與![]() 互素。但是互素的整數中,可以不一定有素數,如
互素。但是互素的整數中,可以不一定有素數,如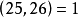 。
。

