原理
整數分拆問題是一個古老而又十分有趣的問題。所謂整數的分拆 ,指將一個正整數表示為若干個正整數的和。
分類
根據是否考慮分拆部分之間的排列順序,我們可以將整數分拆問題分為有序分拆(composition)和無序分拆(partition)。兩者之間的區別如下:
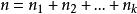 整數分拆
整數分拆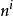 整數分拆
整數分拆在有序分拆中,考慮分拆部分求和之間的順序。假定 , 之間不同的排序記為不同的方案,稱之為n的有序k拆分,如3的有序2拆分為:3=1+2=2+1。我們可以將這個問題建模為排列組合中的“隔板”問題,即n個無區別的球分為r份且每份至少有一個球,則需要用r-1個隔板插入到球之間的n-1個空隙,因此總共的方案數為C(n-1,r-1)。
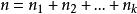 整數分拆
整數分拆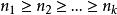 整數分拆
整數分拆在無序拆分中,不考慮其求和的順序。一般假定 , ,我們稱之為n的無序k拆分,如3的無序k拆分為:3=1+2。這種拆分可以理解為將n個無區別的球分為r份且每份至少有一個球。
一般情況下,無序拆分的個數用 p(n) 表示,則 p(2)=1,p(3)=2,p(4)=4。
在通常情況下,整數分拆是指整數的無序分拆。
例子
例1 有1克、2克、3克、4克的砝碼各一枚,問能稱出多少重量,並各有幾種稱法。
該問題可以看成n拆分成1,2,3,4之和且不允許重複的拆分數,利用母函式計算如下:
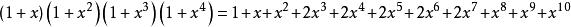 整數分拆
整數分拆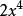 整數分拆
整數分拆表示稱出4克有2種方案,是1+3和2+2,以此類推,超出10克便無法稱出。
 整數分拆
整數分拆例2 將14分拆成兩個自然數的和,並使這兩個自然數的積最大,應該如何分拆?分析與解 不考慮加數順序,將14分拆成兩個自然數的和,有1+13,2+12,3+11,4+10,5+9,6+8,7+7共七種方法。經計算,容易得知,將14分拆成7+ 7時,有最大積7×7=49。
例3 將15分拆成兩個自然數的和,並使這兩個自然數的積最大,如何分拆?
分析與解 不考慮加數順序,可將15分拆成下列形式的兩個自然數的和:1+14,2+13,3+12,4+11,5+10,6+9,7+8。顯見,將15分拆成7+8時,有最大積7×8=56。
註:從上述兩例可見,將一個自然數分拆成兩個自然數的和時,如果這個自然數是偶數2m,當分拆成m+m時,有最大積m×m=m2;如果這個自然數是奇數2m+1,當分拆成m+(m+1)時,有最大積m×(m+1)。
例4 將14分拆成3個自然數的和,並使這三個自然數的積最大,如何分拆?
分析與解 顯然,只有使分拆成的數之間的差儘可能地小(比如是0或1),這樣得到的積才最大。這樣不難想到將14分拆成4+5+5時,有最大積4×5×5=100。
拆分數估計
歷史上,有很多關於整數拆分的研究,其中包括英國劍橋大學的G.E哈代和印度學者拉馬努金,拉馬努拉和哈代通過自己的研究,找到了一個相關的漸進的公式,描述如下。
正整數n拆分成若干個正整數之和,其不同的拆分數用p(n)表示,{p(n)}的母函式為:
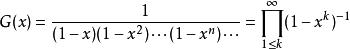 整數分拆
整數分拆則拆分數估計可以表示為:
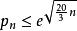 整數分拆
整數分拆拆分數估計定理證明
令
根據馬克羅林級數:
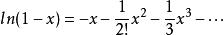 整數分拆
整數分拆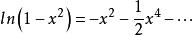 整數分拆
整數分拆 整數分拆
整數分拆所以:
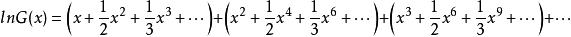 整數分拆
整數分拆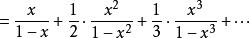 整數分拆
整數分拆而
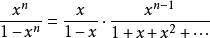 整數分拆
整數分拆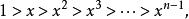 整數分拆
整數分拆又由於
所以
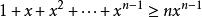 整數分拆
整數分拆故
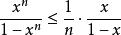 整數分拆
整數分拆所以
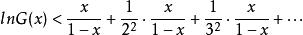 整數分拆
整數分拆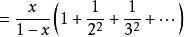 整數分拆
整數分拆但
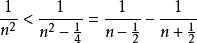 整數分拆
整數分拆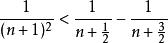 整數分拆
整數分拆 整數分拆
整數分拆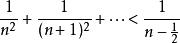 整數分拆
整數分拆所以
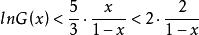 整數分拆
整數分拆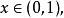 整數分拆
整數分拆設 有
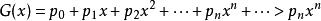 整數分拆
整數分拆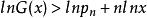 整數分拆
整數分拆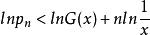 整數分拆
整數分拆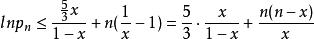 整數分拆
整數分拆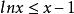 整數分拆
整數分拆曲線 y = lnx 是向上凸的,所以曲線 y = lnx 在(1,0)的切線為 y = x-1 ,即有
所以
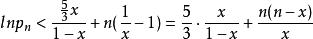 整數分拆
整數分拆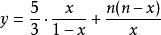 整數分拆
整數分拆對於 求極小值:
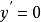 整數分拆
整數分拆令其一階導 ,方程的解為
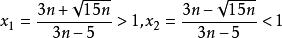 整數分拆
整數分拆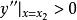 整數分拆
整數分拆又因為y的二階導 ,所以y的極小值為
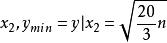 整數分拆
整數分拆所以
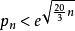 整數分拆
整數分拆拆分數性質
性質一
整數n拆分成最大數為k的拆分數,和數n拆分成k個數的和的拆分數相等。
性質二
整數n拆分成最多不超過m個數的和的拆分數,和n拆分成最大不超過m的拆分數相等。
性質三
整數n拆分成互不相同的若干奇數的和的拆分數,和n拆分成自共軛的Ferrers圖像的拆分數相等。
拆分數計算方法
整數拆分可以利用漸進公式計算,隨著N的無限大,整數拆分估算值接近實際值,現代還可以利用計算機的方法進行求解。在這裡,主要介紹4中計算方法。
遞推法
根據n和m的關係,考慮下面幾種情況:
(1)當n=1時,不論m的值為多少(m>0),只有一種劃分,即{1};
 整數分拆
整數分拆(2)當m=1時,不論 的值為多少(n>0),只有一種劃分,即{1,1,....1,1,1};
(3)當n=m時,根據劃分中是否包含n,可以分為兩種情況:
(a)劃分中包含n的情況,只有一個,即{n};
(b)劃分中不包含n的情況,這時劃分中最大的數字也一定比n小,即n的所有(n-1)劃分;
因此,f(n,n) = 1 + f(n, n - 1)。
(4)當n<m時,由於劃分中不可能出現負數,因此就相當於f(n,n);
(5)當n>m時,根據劃分中是否包含m,可以分為兩種情況:
 整數分拆
整數分拆(a)劃分中包含 的情況,即{m,{x1,x2,x3,...,xi}},其中{x1,x2,x3,...,xi}的和為n-m,可能再次出現m,因此是(n-m)的m劃分,因此這種劃分個數為f(n-m,m;
(b)劃分中不包含m的情況,則劃分中所有值都比m小,即n的(m-1)劃分,個數為f(n,m-1;
因此,f(n,m)=f(n-m,m)+f(n,m-1) 。
綜合以上各種情況,可以看出,上面的結論具有遞歸定義的特徵,其中(1)和(2)屬於回歸條件,(3)和(4)屬於特殊情況,而情況(5)為通用情況,屬於遞歸的方法,其本質主要是通過減少n或m以達到回歸條件,從而解決問題。
詳細遞推公式描述如下:
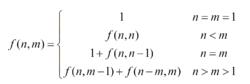 整數分拆
整數分拆參考源碼
這個版本的時間複雜度較高,運行效率很低。
動態規劃法
考慮到在上一節使用遞歸中,很多的子遞歸重複計算。如在計算 f (10,9)時,劃分成為 f (1,9) + f (10,8),進一步劃分為 f (1,1)=f (2,8)+f (10,7),接下來轉換為f (1,1) +f (2,2)+ f (3,7)+ f (10,6) =3* f (1,1) +1+ f (3,7)+ f (10,6),這樣就產生了重複,然而,在遞歸的時候,每個都需要被計算一遍,因此可見,位於底層的狀態,計算的次數也越來越多。這樣在時間開銷特別大,是造成運算慢的根本原因,比如算120的時候需要3秒中,計算130的時候需要27秒鐘,在計算機200的時候....計算10分鐘還沒計算出來。
鑒於此,我們已經分析出了普通遞推關係中存在大量的冗餘造成了重複計算,最終導致了運行時間太長,一種自然地想法是能夠用一種技巧,以避免重複計算?這裡我們使用動態規劃的思想進行程式設計。
在上一節中,已經分析了狀態轉移的方程,因此,我們在求解子問題時,利用標記的思想,首先檢查產生的子問題是否在之前被計算過,這是因為對於相同的子問題,得到的結果肯定是一樣的,因此利用這一步去掉冗餘的操作,極大減少了計算的時間開銷。對於沒有標記的子問題來說,一定是沒有被計算過,這樣,在計算完成後,順便標記一下子問題,以確保以後不用再重複計算。利用這個特性,可以確保所有的劃分子問題都無重複,無遺漏的恰巧被計算一次。
動態規劃版主要是利用了標記思想進行加速。
參考源碼如下:
這樣的算法效率快了很多。
生成函式法
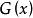 整數分拆
整數分拆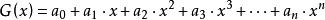 整數分拆
整數分拆對於整數拆分問題,也可以從另一個角度,即“母函式”的角度來考慮這個問題。所謂母函式,即為關於x的一個多項式 ,滿足:
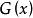 整數分拆
整數分拆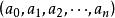 整數分拆
整數分拆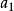 整數分拆
整數分拆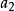 整數分拆
整數分拆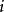 整數分拆
整數分拆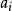 整數分拆
整數分拆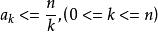 整數分拆
整數分拆則我們稱為序列 的母函式。我們從整數劃分考慮,假設的某個劃分中,1的出現個數記為 ,2的個數記為 ,…, 的個數 記為顯然有:
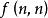 整數分拆
整數分拆 整數分拆
整數分拆 整數分拆
整數分拆 整數分拆
整數分拆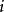 整數分拆
整數分拆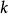 整數分拆
整數分拆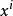 整數分拆
整數分拆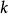 整數分拆
整數分拆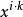 整數分拆
整數分拆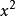 整數分拆
整數分拆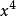 整數分拆
整數分拆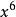 整數分拆
整數分拆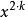 整數分拆
整數分拆 整數分拆
整數分拆因此 的劃分數,也就是從1到 這 個數字的組合,每個數字理論上可以無限重複出現,即個數隨意,使它們的和為 。顯然,數字 可以有如下可能,出現0次(即不出現),1次,2次,…, 次等等。把數字用 表示,出現 次的數字用 表示,不出現用1表示。例如,數字2用 表示,2個2用 表示,3個2用 表示,k個2用 表示。則對於從1到 的所有可能組合結果我們可以表示為:
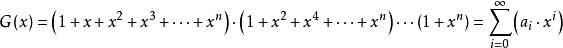 整數分拆
整數分拆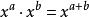 整數分拆
整數分拆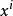 整數分拆
整數分拆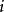 整數分拆
整數分拆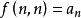 整數分拆
整數分拆上面的表達式中,每個括弧內的多項式代表了數字的參與到劃分中的所有可能情況。因此,該多項式展開後,由於 ,因此 就代表了 的劃分,展開後項的係數也就是的所有劃分個數,即 。
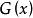 整數分拆
整數分拆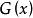 整數分拆
整數分拆 整數分拆
整數分拆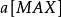 整數分拆
整數分拆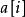 整數分拆
整數分拆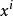 整數分拆
整數分拆由此我們找到了關於整數劃分的母函式 ,剩下的問題就是,我們需要求出 的展開後的所有係數。為此,我們首先要做多項式乘法,對於計算機編程來說,並不困難。我們把一個關於 的多項式用一個整數數組 表示, 代表 的係數,然後卷積即可。
參考源碼:
這樣基於生成函式的方法實際上快了很多。
五邊形數法
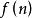 整數分拆
整數分拆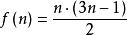 整數分拆
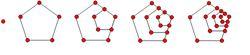
整數分拆設第n個五邊形數為 ,那么 ,即序列為:1, 5, 12, 22, 35, 51, 70, ...
對應圖形如下:
 整數分拆
整數分拆設五邊形數的生成函式為,那么有:
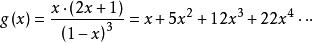 整數分拆
整數分拆以上是五邊形數的情況。下面是關於五邊形數定理的內容:
五邊形數定理是一個由歐拉發現的數學定理,描述歐拉函式展開式的特性。歐拉函式的展開式如下:
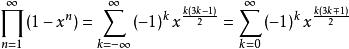 整數分拆
整數分拆即:
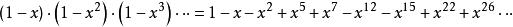 整數分拆
整數分拆可見,歐拉函式展開後,有些次方項被消去,只留下次方項為1, 2, 5, 7, 12, ...的項次,留下來的次方恰為廣義五邊形數。
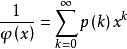 整數分拆
整數分拆五邊形數和分割函式的關係:歐拉函式的倒數是分割函式的母函式,亦即:
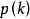 整數分拆
整數分拆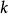 整數分拆
整數分拆其中 為 的分割函式。上式配合五邊形數定理,有:
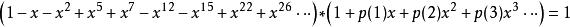 整數分拆
整數分拆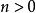 整數分拆
整數分拆在 時,等式右側的係數均為0,比較等式二側的係數,可得
 整數分拆
整數分拆因此可得到分割函式的遞歸式:
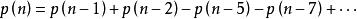 整數分拆
整數分拆所以,通過上面遞歸式,我們可以很快速地計算的整數劃分方案數了。
參考代碼:
以上設計的代碼是最高效的。
通過比較上述四種算法,可見整數拆分的劃分方法比較多樣,且不同的算法運行效率差距比較大,需要仔細理解和思考。

