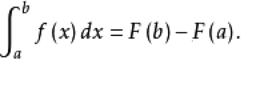定理定義
定義
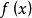牛頓-萊布尼茨公式
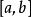牛頓-萊布尼茨公式
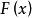牛頓-萊布尼茨公式如果函式 在區間 上連續，並且存在原函式 ，
則
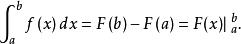牛頓-萊布尼茨公式弱化條件
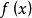牛頓-萊布尼茨公式 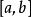牛頓-萊布尼茨公式如果函式 區間 上有定義，並且滿足以下條件：
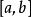牛頓-萊布尼茨公式（1）在區間 上可積；
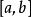牛頓-萊布尼茨公式 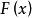牛頓-萊布尼茨公式（2）在區間 上存在原函式 ；
則
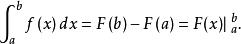牛頓-萊布尼茨公式公式推導
推導一
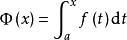牛頓-萊布尼茨公式
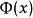牛頓-萊布尼茨公式
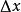牛頓-萊布尼茨公式定義一個變上限積分函式 ，讓函式 獲得增量 ，則對應的函式增量
牛頓-萊布尼茨公式根據積分中值定理可得，
牛頓-萊布尼茨公式，（ξ在x與x+Δx之間）
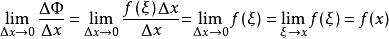牛頓-萊布尼茨公式，
所以
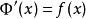牛頓-萊布尼茨公式
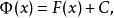牛頓-萊布尼茨公式，
因為
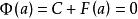牛頓-萊布尼茨公式
牛頓-萊布尼茨公式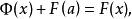
牛頓-萊布尼茨公式，所以 ，即
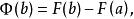牛頓-萊布尼茨公式所以
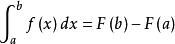牛頓-萊布尼茨公式即
證畢。
推導二
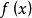牛頓-萊布尼茨公式 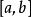牛頓-萊布尼茨公式 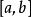牛頓-萊布尼茨公式因為函式在區間 上可積，任取區間 的分割
牛頓-萊布尼茨公式
牛頓-萊布尼茨公式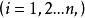
牛頓-萊布尼茨公式
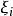牛頓-萊布尼茨公式在區間 上任取一點 ，則有
牛頓-萊布尼茨公式
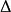牛頓-萊布尼茨公式其次，對於分割 ，有
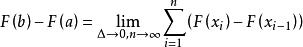牛頓-萊布尼茨公式 牛頓-萊布尼茨公式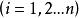
牛頓-萊布尼茨公式 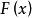牛頓-萊布尼茨公式在區間 上對函式 套用拉格朗日中值定理得
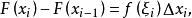牛頓-萊布尼茨公式
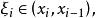牛頓-萊布尼茨公式其中 因此有
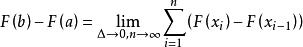牛頓-萊布尼茨公式
牛頓-萊布尼茨公式證畢。
定理推廣
二重積分形式
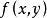牛頓-萊布尼茨公式
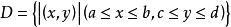牛頓-萊布尼茨公式
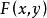牛頓-萊布尼茨公式設函式 在矩形區域 上連續，如果存在一個二元函式 ，使得
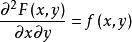牛頓-萊布尼茨公式，
牛頓-萊布尼茨公式則二重積分
曲線積分形式
與格林公式和高斯公式的聯繫
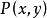牛頓-萊布尼茨公式
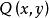牛頓-萊布尼茨公式設 D為單連通區域， 與 在區域 D上有連續的一階偏導數，
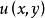牛頓-萊布尼茨公式若存在一個二元函式 ，使得
牛頓-萊布尼茨公式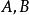
牛頓-萊布尼茨公式 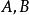牛頓-萊布尼茨公式在區域 D中任意取兩個點 ，則對連線 的任意一條光滑曲線 L，
都有
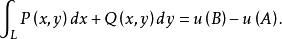牛頓-萊布尼茨公式發展簡史
牛頓-萊布尼茨公式1670年，英國數學家伊薩克·巴羅在他的著作《幾何學講義》中以幾何形式表達了切線問題是面積問題的逆命題，這實際是牛頓-萊布尼茨公式的幾何表述。
1666年10月，牛頓在它的第一篇微積分論文《流數簡論》中解決了如何根據物體的速度求解物體的位移這一問題，並討論了如何根據這種運算求解曲線圍成的面積，首次提出了微積分基本定理。
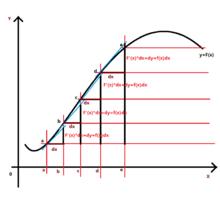
德國數學家萊布尼茨在研究微分三角形時發現曲線的面積依賴於無限小區間上的縱坐標值和，1677年，萊布尼茨在一篇手稿中明確陳述了微積分基本定理：給定一個曲線，其縱坐標為y，如果存在一條曲線z，使得dz/dx=y，則曲線y下的面積∫ydx=∫dz=z。
定理意義
牛頓-萊布尼茨公式的發現，使人們找到了解決曲線的長度，曲線圍成的面積和曲面圍成的體積這些問題的一般方法。它簡化了定積分的計算，只要知道被積函式的原函式，總可以求出定積分的精確值或一定精度的近似值。
牛頓-萊布尼茨公式是聯繫微分學與積分學的橋樑，它是微積分中最基本的公式之一。它證明了微分與積分是可逆運算，同時在理論上標誌著微積分完整體系的形成，從此微積分成為一門真正的學科。
牛頓-萊布尼茨公式是積分學理論的主幹，利用牛頓一萊布尼茨公式可以證明定積分換元公式，積分第一中值定理和積分型餘項的泰勒公式。牛頓-萊布尼茨公式還可以推廣到二重積分與曲線積分，從一維推廣到多維。
公式套用
牛頓-萊布尼茨公式簡化了定積分的計算，利用該公式可以計算曲線的弧長，平面曲線圍成的面積以及空間曲面圍成的立體體積，這在實際問題中有廣泛的套用，例如計算壩體的填築方量。
牛頓-萊布尼茨公式在物理學上也有廣泛的套用，計算運動物體的路程，計算變力沿直線所做的功以及物體之間的萬有引力。
牛頓-萊布尼茨公式促進了其他數學分支的發展，該公式在微分方程，傅立葉變換，機率論，複變函數等數學分支中都有體現。
