定義
點列的強收斂
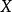 強收斂
強收斂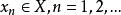 強收斂
強收斂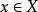 強收斂
強收斂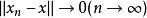 強收斂
強收斂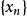 強收斂
強收斂 強收斂
強收斂設是賦范線性空間, ,如果存在,使得 ,則稱點列 強收斂於。
點列的弱收斂
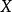 強收斂
強收斂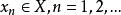 強收斂
強收斂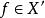 強收斂
強收斂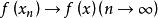 強收斂
強收斂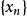 強收斂
強收斂 強收斂
強收斂設是賦范線性空間, ,若對任意的 ,都有 ,則稱點列弱收斂於。
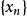 強收斂
強收斂 強收斂
強收斂 強收斂
強收斂若點列弱收斂於,則弱極限存在且只有一個。
關係:強收斂必定弱收斂,但弱收斂不一定強收斂。
X與其共軛空間中運算元列的收斂性
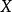 強收斂
強收斂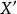 強收斂
強收斂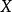 強收斂
強收斂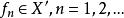 強收斂
強收斂設是賦范線性空間,是的共軛空間,泛函列 。
運算元列的強收斂
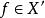 強收斂
強收斂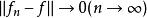 強收斂
強收斂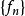 強收斂
強收斂 強收斂
強收斂若存在 ,使得 ,則稱 強收斂於。
運算元列的弱*收斂
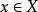 強收斂
強收斂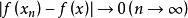 強收斂
強收斂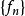 強收斂
強收斂 強收斂
強收斂若對任意的 ,都有 ,則稱點列 弱*收斂於。
運算元列的弱收斂
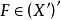 強收斂
強收斂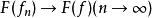 強收斂
強收斂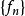 強收斂
強收斂 強收斂
強收斂若對任意的 ,都有 ,則稱點列 弱收斂於。
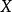 強收斂
強收斂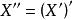 強收斂
強收斂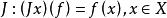 強收斂
強收斂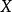 強收斂
強收斂弱*收斂與弱收斂一般不一致,但如果和之間能夠建立起等距同構: ,則稱是自反的,在自反空間中,這兩種收斂就是等價的。
X與Y空間中運算元列的收斂性
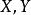 強收斂
強收斂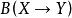 強收斂
強收斂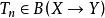 強收斂
強收斂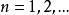 強收斂
強收斂設是兩個賦范線性空間, 表示X到Y中的有界線性運算元全體所成的空間,。
運算元列的一致收斂
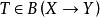 強收斂
強收斂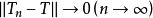 強收斂
強收斂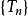 強收斂
強收斂 強收斂
強收斂若存在 ,使得 ,則稱運算元列 一致收斂於。
運算元列的強收斂
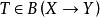 強收斂
強收斂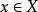 強收斂
強收斂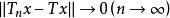 強收斂
強收斂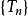 強收斂
強收斂 強收斂
強收斂若存在 ,使得對任意的,都有 ,則稱運算元列 強收斂於。
運算元列的弱收斂
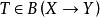 強收斂
強收斂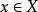 強收斂
強收斂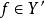 強收斂
強收斂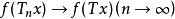 強收斂
強收斂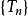 強收斂
強收斂 強收斂
強收斂若存在 ,使得對任意的和任意的,有 ,則稱運算元列 弱收斂於。
關係:顯然有運算元的一致收斂可導出強收斂,由強收斂可導出弱收斂,反之不然。

