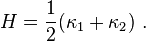平均曲率

在微分幾何中，一個曲面 S 的平均曲率（mean curvature）H，是一個“外在的”彎曲測量標準，局部地描述了一個曲面嵌入周圍空間（比如二維曲面嵌入三維歐幾里得空間）的曲率。

概述

在微分幾何中，一個曲面 S 的平均曲率（mean curvature）H，是一個“外在的”彎曲測量標準，局部地描述了一個曲面嵌入周圍空間（比如二維曲面嵌入三維歐幾里得空間）的曲率。

這個概念由索菲·熱爾曼在她的著作《彈性理論》中最先引入。

定義

令p是曲面S上一點考慮S上過p的所有曲線Ci。每條這樣的Ci在p點有一個伴隨的曲率Ki在這些曲率Ki中，至少有一個極大值κ1 與極小值κ2這兩個曲率κ1,κ2稱為S的主曲率。

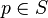p\in S的平均曲率是兩個主曲率的平均值(斯皮瓦克 1999, 第3卷，第2章)，由歐拉公式其實也是所有曲率的平均值[3]，故有此名。

H = {1 \over 2} (\kappa_1 + \kappa_2)\ .
利用第一基本形式與第二基本形式的係數，平均曲率表示為：

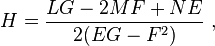
H =\frac{LG-2MF+NE}{2(EG-F^2)}\ ,
這裡 E,F,G 是第一基本形式的係數，L,M,N 為第二基本形式的係數。

平均曲率可推廣為更一般情形 (斯皮瓦克 1999, 第4卷，第7章)，一個超曲面 T 的平均曲率為：

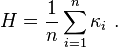
H=\frac{1}{n}\sum_{i=1}^{n} \kappa_{i}\ .
更抽象地說，平均曲率是第二基本形式（或等價地，形運算元）的跡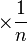\times\frac{1}{n} 。

另外，平均曲率 H 可以用共變導數\nabla 寫成

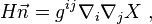
H\vec{n} = g^{ij}\nabla_i\nabla_j X\ ,
這裡利用了高斯-Weingarten 關係，X(x,t) 是一族光滑嵌入超曲面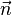，\vec{n} 為單位法向量，而gij 是度量張量。

一個曲面是極小曲面若且唯若平均曲率為零。此外，平面 S 平均曲率滿足一個熱型方程稱為平均曲率流方程。

3 維空間中曲面

對 3 維空間中的曲面，平均曲率與曲面的單位法向量相關：

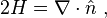
2 H = \nabla \cdot \hat n\ ,
這裡法向量的選取影響曲率的正負號。曲率的符號取決於法向量的方向：如果曲面“遠離”法向量則曲率是正的。上面的公式對 3 維空間中任何方式定義的曲面都成立，只要能夠計算單位法向量的散度。

對曲面是兩個坐標的函式定義的曲面，比如 z = S(x,y)，使用向下的法向量平均曲率（的兩倍）表示為

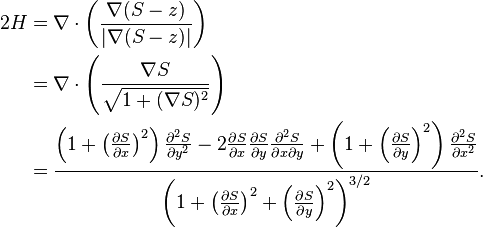
\begin{align}2 H & = \nabla \cdot \left(\frac{\nabla(S - z)}{|\nabla(S - z)|}\right) \\& = \nabla \cdot \left(\frac{\nabla S}{\sqrt{1 + (\nabla S)^2}}\right) \\& = \frac{\left(1 + \left(\frac{\partial S}{\partial x}\right)^2\right) \frac{\partial^2 S}{\partial y^2} - 2 \frac{\partial S}{\partial x} \frac{\partial S}{\partial y} \frac{\partial^2 S}{\partial x \partial y} + \left(1 + \left(\frac{\partial S}{\partial y}\right)^2\right) \frac{\partial^2 S}{\partial x^2}}{\left(1 + \left(\frac{\partial S}{\partial x}\right)^2 + \left(\frac{\partial S}{\partial y}\right)^2\right)^{3/2}}.\end{align}
如果曲面還是軸對稱的，滿足 z = S(r)，則

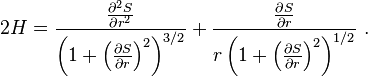
2 H = \frac{\frac{\partial^2 S}{\partial r^2}}{\left(1 + \left(\frac{\partial S}{\partial r}\right)^2\right)^{3/2}} + \frac{\frac{\partial S}{\partial r}}{r \left(1 + \left(\frac{\partial S}{\partial r}\right)^2\right)^{1/2}}\ .

流體力學

在流體力學中使用的另外一種定義是不要因子 2：

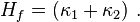
H_f = (\kappa_1 + \kappa_2)\ .
這出現於楊-拉普拉斯方程中，平衡球狀小滴內部的壓力等於表面張力乘以 Hf；兩個曲率等於小滴半徑的倒數 κ1 = κ2 = r ^-1。

極小曲面

Costa 極小曲面示意圖

平均曲率

一個極小曲面是所有點的平均曲率為零的曲面。經典例子有懸鏈面、螺鏇面、Scherk 曲面與 Enneper 曲面。新近發現的包括 Costa 極小曲面（Costa's mimimal surface，1982年）與 Gyroid（Gyroid，1970年）。

極小曲面的一個推廣是考慮平均曲率為非零常數的曲面，球面和圓柱面就是這樣的例子。Heinz Hopf 的一個問題為是否存在曲率為非零常數的非球面閉曲面。球面是惟一具有常平均曲率且沒有邊界或奇點的曲面；如果允許自交，則存在平均曲率為非零常數的閉曲面，Wente 在1986年曾構造出這樣的自交環面(陳維桓 2006, 4.6節)。

參見

高斯曲率
平均曲率流
逆平均曲率流
面積公式第一變分

注釋

Dubreil-Jacotin on Sophie Germain
Curvature in the Calculus Curriculum
關於角度的平均值。

參考文獻

斯皮瓦克, 麥可 (1999), A comprehensive introduction to differential geometry (Volumes 3-4) (3rd ed.), Publish or Perish Press, ISBN 0-914098-72-1 (Volume 3), ISBN 0-914098-73-X (Volume 4).
陳維桓 (2006), 微分幾何, 北京大學出版社, ISBN 7-307-10709-9

相關搜尋

熱門詞條

聯絡我們