基本內容
實數根也經常被叫為實根.
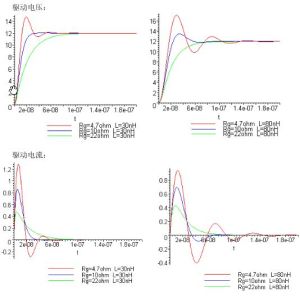實根是個過阻尼1)根指的是方程的解
實根就是指方程式的解為實數
2)實數包括正數，負數和0
複數包括：實數和虛數
實數包括：有理數和無理數
有理數包括：整數和分數
無理數包括：正無理數、負無理數
整數包括：正整數、0、負整數
分數包括：正分數、負分數
分數的第二種分類方法：包括有限小數、無限循環小數
3）有理數：整數和分數統稱為有理數。
無理數：無限不循環小數叫做無理數，具體表示方法為√2、√3。
有關定理
定理1 1 次多項式至多有個不同的根
定理2 笛卡爾符號律2 多項式函式的正實根個數等於的非零係數的符號變化個
數或者等於比該變化個數小一個偶數的數的負實根個數等於的非零係數的符號變化個
數或者等於比該變化個數小一個偶數的數
定理3 1 數是的根的充分必要條件是能被整除
定理4 1 每個次數大於0 的實係數多項式都可以分解為實係數的一次和二次不可約因式的乘積
定理5 1 設1 式中P0 1 *∈ 即是整係數多項式若≠0 且有理數
是的一個根∈ ∈ * 1 那么
i 0
(ii) 是一個整係數多項式
定理6 根的上下界定理2 設1 式中0 0
1 若存在正實數當用去對作綜合除法時第三行數字僅出現正數或0 那么就
是的根的一個上界
2 若存在不大於0 的實數當用去對作綜合除法時第三行數字交替地出現正數或
0 和負數或0 時那么就是的根的一個下界
定理7 判斷根上下界的牛頓法3 設有實數使**均為非負
數或均為非正數則方程0 的實根都小於這裡表示的階導數
定理8 判斷根上下界的拉格朗日法3 設1 式中0 0 且為第一個負係數即0 且P≥0 設是負係數中的最大絕對值則0 的正根上限為1
0
定理9 1 多項式無重根的充分且必要條件是與它的導數互素
定理10 Sturm 定理3 設多項式無重根1 2 1 2 ≠0 0 在開區間
1 2 中有個根1 與2 分別為的斯圖姆St urm序列
0 1 1 1 *1 *1
與0 2 1 2 *2 *2
的變號的個數則1 2
定理11 3 設為實係數多項式為的根的判別式則當0 時方程
0 有重根當0 時方程0 無重根且有奇數對虛根當0 時方程0 無
重根且有偶數對虛根
對1 式中的定義為
1 1 2 1
0
其中為的導函式稱為和的結式是由的各項係數確定的一個2 1 階方
陣R 的行列式. 如果當或0 時記0 則R 的第行第列的元素為
當1 ≤≤1
1 1 當≤≤2 1 時
有關定理
定理1 [1 ] n 次多項式f ( x ) 至多有n 個不同的根.
定理2 (笛卡爾符號律) [2 ] 多項式函式f ( x ) 的正實根個數等於f ( x ) 的非零係數的符號變化個
數,或者等於比該變化個數小一個偶數的數; f ( x ) 的負實根個數等於f ( - x) 的非零係數的符號變化個
數,或者等於比該變化個數小一個偶數的數.
定理3 [1 ] 數c 是f ( x ) 的根的充分必要條件是f ( x ) 能被x - c 整除.
定理4 [1 ] 每個次數大於0 的實係數多項式都可以分解為實係數的一次和二次不可約因式的乘積.
定理5 [1 ] 設(1 ) 式中Pi = 0 ,1 ,*,n , ai ∈ ,即f ( x ) 是整係數多項式,若an ≠0 ,且有理數u/ v
是f ( x ) 的一個根, u ∈ , v ∈ * ,( u , v) = 1 ,那么:
(i ) v | a0 , u | an ;
(ii) f ( x ) / ( x - u/ v) 是一個整係數多項式.
定理6 (根的上下界定理) [2 ] 設(1 ) 式中a0 > 0 ,
1 ) 若存在正實數M ,當用x - M 去對f ( x ) 作綜合除法時第三行數字僅出現正數或0 ,那么M 就
是f ( x ) 的根的一個上界;
2 ) 若存在不大於0 的實數m ,當用x - m 去對f ( x ) 作綜合除法時第三行數字交替地出現正數(或
0 ) 和負數(或0 ) 時,那么m 就是f ( x ) 的根的一個下界.
定理7 (判斷根上下界的牛頓法) [3 ] 設有實數k ,使f ( k) , f ′(k) , *,f (m) ( k) , *f (n) ( k) 均為非負
數,或均為非正數,則方程f ( x ) = 0 的實根都小於k. 這裡f (m) ( x ) 表示f ( x ) 的m 階導數.
定理8 (判斷根上下界的拉格朗日法) [3 ] 設(1 ) 式中a0 > 0 ,且ak 為第一個負係數,即ak < 0 ,且Pi < k , ai ≥0 , 設b 是負係數中的最大絕對值,則f ( x ) = 0 的正根上限為1 +
k
b/ a0 .
定理9 [1 ] 多項式f ( x ) 無重根的充分且必要條件是f ( x ) 與它的導數f ′( x ) 互素.
定理10 (Sturm 定理) [3 ] 設多項式f ( x ) 無重根,b1 < b2 , f (b1 ) f (b2 ) ≠0 , f ( x ) = 0 在開區間
(b1 ,b2 ) 中有p 個根,U (b1 ) 與U (b2 ) 分別為f ( x ) 的斯圖姆(St urm) 序列
f 0 (b1 ) , f 1 (b1 ) , *,f s (b1 ) , *,f m (b1 )
與f 0 (b2 ) , f 1 (b2 ) , *,f s (b2 ) , *,f m (b2 )
的變號的個數,則p = U (b1 ) - U (b2 ) .
定理11 [3 ] 設f ( x ) 為實係數多項式,D ( f ) 為f ( x ) 的根的判別式,則當D ( f ) = 0 時,方程f ( x )
= 0 有重根;當D ( f ) < 0 時,方程f ( x ) = 0 無重根,且有奇數對虛根;當D ( f ) > 0 時方程f ( x ) = 0 無
重根,且有偶數對虛根.
對(1 ) 式中的f ( x ) , D ( f ) 定義為:
D( f ) = (- 1 ) n(n - 1 )/ 2 a- 1
0 R ( f , f ′) ,
其中f′為f ( x ) 的導函式, R ( f , f ′) 稱為f 和f ′的結式,是由f ( x ) 的各項係數確定的一個2 n - 1 階方
陣R 的行列式. 如果當k > n 或k < 0 時記ak = 0 , 則R 的第i 行第j 列的元素為
rij =
aj - i , 當1 ≤i ≤n - 1 ;
(i - j + 1 )aj+n- i- 1 , 當n ≤i ≤2 n - 1 時
