簡介
 完全圖
完全圖當然不一樣了,n個頂點的完全圖有n(n-1)/2條邊;而連通圖則不一定,但至少有n-1條邊.舉個例子,四個頂點的完全圖有6條邊,也就是四條邊加上2條對角線;而連通圖可以只包含周圍四條邊就可以了。
無向完全圖
任意一個具有n個結點的無向簡單圖,其邊數小於等於n*(n-1)/2;我們把邊數恰好等於n*(n-1)/2的n個結點的無向圖稱為完全圖。
有向完全圖
在一個n個結點的有向圖中,最大邊數為n*(n-1)。
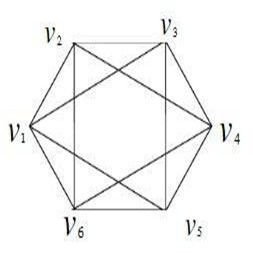
完全圖,所有完全圖都是它本身的團。若一個圖的每一對不同頂點恰有一條邊相連,則稱為完全圖。完全圖是每對頂點之間都恰連有一條邊的簡單圖。n個端點的完全圖有n個端點及n(n−1)/2條邊,以Kn表示。它是(k−1)-正則圖。所有完全圖都是它本身的團(clique)。
 完全圖
完全圖任意一個具有n個結點的無向簡單圖,其邊數小於等於n*(n-1)/2;我們把邊數恰好等於n*(n-1)/2的n個結點的無向圖稱為完全圖。
在一個n個結點的有向圖中,最大邊數為n*(n-1)。
