半序線性空間
正文
一類賦有序關係的線性空間,稱為有序線性空間。如果只考察實值函式,則重要的空間如C(Ω),Lp(Ω)(1≤p<∞),除了有線性結構、拓撲結構以外,還有個按照自然的序:
ƒ≥0,若ƒ(t)≥0對一切(幾乎所有)t∈Ω都成立,構成的序結構。某些空間中的這種序或“正性”,在理論和套用上都是很重要的。
半序空間與向量格 如果實線性空間E的某些元素偶(x,y)之間有關係x≥y,並存在①序關係;x≥x,又 x≥y 且
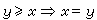 ,x≥y 且
,x≥y 且 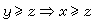 ;②
;②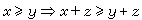 ,x≥y,
,x≥y,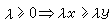 ;則稱E為半序線性空間。若進而還有③格關係:對x、y∈E恆有z∈E,使x≤z且y≤z,又x≤u,
;則稱E為半序線性空間。若進而還有③格關係:對x、y∈E恆有z∈E,使x≤z且y≤z,又x≤u,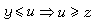 。就稱E為向量格或里斯空間,且記③中之z為x∨y。
。就稱E為向量格或里斯空間,且記③中之z為x∨y。 一般對具有性質①的集合,稱為按關係≥是半序的,而上述性質②則意線上性結構與序結構的協調。
向量格實例 ①設CR(Ω)是緊豪斯多夫空間Ω上全體實值連續函式,其上的加法與數乘如通常定義。對 x、y∈C(Ω)定義
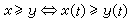 ,當t∈Ω。這時(x∨y)(t)=max{x(t),y(t)},易見 CR(Ω)是向量格。②設(x,B)是可測空間。設V是全體在(x,B)上有限的,完全可加的集合函式。對μ1,μ2∈V 及實數α定義
,當t∈Ω。這時(x∨y)(t)=max{x(t),y(t)},易見 CR(Ω)是向量格。②設(x,B)是可測空間。設V是全體在(x,B)上有限的,完全可加的集合函式。對μ1,μ2∈V 及實數α定義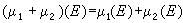 ,E∈B;
,E∈B;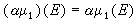 ,E∈B,α是實的;
,E∈B,α是實的;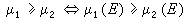 ,E∈B。這時,
,E∈B。這時, 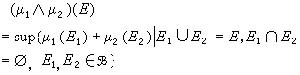
當E∈B。可以證明,V是向量格。③對希爾伯特空間H上有界線性運算元A與B,如果對任何有界的T使AT=TA皆有BT=TB,則稱B堻堻A。設 A是H上給定的有界自伴運算元,令RA={H;B

 A},定義
A},定義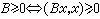 ,當x∈H,則對
,當x∈H,則對 有
有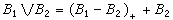 。這裡
。這裡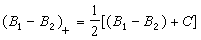 而
而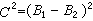 且C≥0,可以證明RA是向量格。
且C≥0,可以證明RA是向量格。 向量格的性質 在向量格中定義
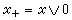 ,x_=(-x)∨0,|x|=x∨(-x)依次稱為x的正部分、負部分、絕對值。在向量格中,每個元x都有若爾當分解
,x_=(-x)∨0,|x|=x∨(-x)依次稱為x的正部分、負部分、絕對值。在向量格中,每個元x都有若爾當分解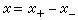 。這是有界變差函式以及抽象測度論中的結果的推廣。
。這是有界變差函式以及抽象測度論中的結果的推廣。 對向量格E中的一族元素
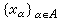 ,若有x∈E,使得x≥xα對一切α∈A成立,又任何y≥yα對一切
,若有x∈E,使得x≥xα對一切α∈A成立,又任何y≥yα對一切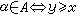 ,則稱x為
,則稱x為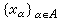 之上確界,記作
之上確界,記作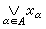 。同樣,可定義下確界
。同樣,可定義下確界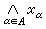 在一般的向量格中,上方有界的點列未必有上確界。如果對Χ之任何上方有界點列
在一般的向量格中,上方有界的點列未必有上確界。如果對Χ之任何上方有界點列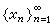 ,必有上確界,則稱Χ 為σ-完備的。前述之向量格V與RA都是σ-完備的。
,必有上確界,則稱Χ 為σ-完備的。前述之向量格V與RA都是σ-完備的。 對E中的點列
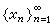 ,若有單調遞減的點列wn使得
,若有單調遞減的點列wn使得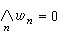 ,而
,而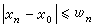 ,則稱xn序收斂於x0,記作
,則稱xn序收斂於x0,記作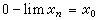 。
。 設Χ為實的巴拿赫空間。如果Χ還是一個向量格,而且
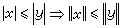 ,
,
利用格序關係與序收斂,對σ-完備的向量格 Χ可定義絕對連續元素與奇異元素,從而將拉東-尼科迪姆定理推廣成:Χ的每個元都可惟一地表示成絕對連續元與奇異元的和。又對某些σ-完備向量格中之元α,可惟一地確定一個單位分解{eλ;-∞<λ<∞},使
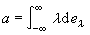 ,從而將自伴運算元譜分解定理推廣到適當的 σ- 完備向量格上。設Χ為巴拿赫格,如果還有x≥0,
,從而將自伴運算元譜分解定理推廣到適當的 σ- 完備向量格上。設Χ為巴拿赫格,如果還有x≥0,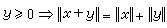 ,則稱Χ為抽象L1空間。可以證明有測度空間Ω使得這種Χ線性的,保范序同構於L(Ω),同樣也可用格序關係與範數刻畫Lp(Ω)與C(K),這裡K是緊空間。
,則稱Χ為抽象L1空間。可以證明有測度空間Ω使得這種Χ線性的,保范序同構於L(Ω),同樣也可用格序關係與範數刻畫Lp(Ω)與C(K),這裡K是緊空間。 參考書目
關肇直編:《泛函分析講義》,高等教育出版社,北京,1958。
A.C.Zaanen and W.A.J.Luxemburg,Riesz Spaces,North-Holland, Amsterdam,1971.