基本介紹
鞅可以用於研究公平賭博(公平博弈),然而,現實生活中的博弈很多時候都是非公平的,此時,就需要藉助上、下鞅的理論,上、下鞅可以解決非公平博弈問題。
 下鞅
下鞅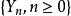 下鞅
下鞅定義1 與 是隨機過程,如果滿足下列條件:
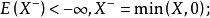 下鞅
下鞅(1)
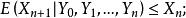 下鞅
下鞅(2)
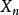 下鞅
下鞅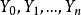 下鞅
下鞅(3) 是 的函式。
 下鞅
下鞅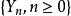 下鞅
下鞅則稱 關於 是一個 上鞅。
 下鞅
下鞅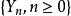 下鞅
下鞅定義2 與 是隨機過程,如果滿足下列條件:
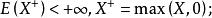 下鞅
下鞅(1)
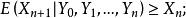 下鞅
下鞅(2)
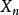 下鞅
下鞅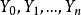 下鞅
下鞅(3) 是 的函式。
 下鞅
下鞅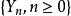 下鞅
下鞅則稱 關於 是一個 下鞅。
下鞅的性質及證明
 下鞅
下鞅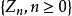 下鞅
下鞅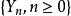 下鞅
下鞅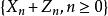 下鞅
下鞅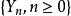 下鞅
下鞅定理 如果 , 關於 是上(下)鞅, 則 關於 是上(下)鞅。
 下鞅
下鞅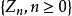 下鞅
下鞅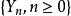 下鞅
下鞅證明:若 , 關於 是上鞅,則:
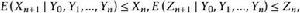 下鞅
下鞅進而
 下鞅
下鞅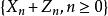 下鞅
下鞅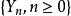 下鞅
下鞅即 關於 是上鞅。
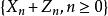 下鞅
下鞅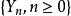 下鞅
下鞅同理,可證 關於 是下鞅。
Jensen不等式與下鞅的構造
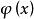 下鞅
下鞅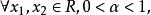 下鞅
下鞅先介紹Jensen不等式,設 為一凸函式,即對 有
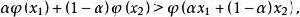 下鞅
下鞅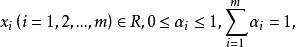 下鞅
下鞅其推廣結果為:對
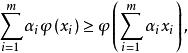 下鞅
下鞅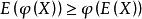 下鞅
下鞅因此, 。
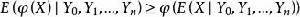 下鞅
下鞅同理, 。
將X換成X,然後利用下鞅的性質可得下面的定理。
 下鞅
下鞅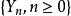 下鞅
下鞅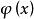 下鞅
下鞅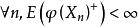 下鞅
下鞅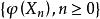 下鞅
下鞅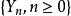 下鞅
下鞅定理1 如果 關於 是鞅, 為一凸函式,且對 ,則 關於 是下鞅。
 下鞅
下鞅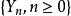 下鞅
下鞅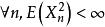 下鞅
下鞅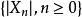 下鞅
下鞅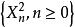 下鞅
下鞅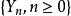 下鞅
下鞅推論1 如果 關於 是鞅,對 ,則 , 關於 是下鞅。
由於絕對值函式和平方函式為凸函式,因此可用任意凸函式構造下鞅。
 下鞅
下鞅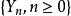 下鞅
下鞅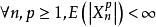 下鞅
下鞅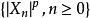 下鞅
下鞅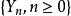 下鞅
下鞅推論2 如果 關於 是鞅,對 ,則 關於 是下鞅。
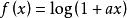 下鞅
下鞅注意: 函式 是關於x的凸函式(convex function),其中a>0,x≥0.
對任意的非負隨機變數X,利用Jensen不等式,於是有
 下鞅
下鞅當然,此函式也可用於下鞅的討論。
鞅分解定理
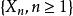 下鞅
下鞅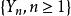 下鞅
下鞅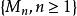 下鞅
下鞅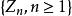 下鞅
下鞅定理 對於任意一個 關於 的下鞅,必存在過程 與 ,使得:
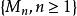 下鞅
下鞅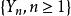 下鞅
下鞅(1) 關於 是鞅;
 下鞅
下鞅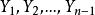 下鞅
下鞅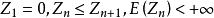 下鞅
下鞅(2) 是 的函式(n≥2),且 ;
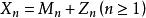 下鞅
下鞅(3) 。
且上述分解是唯一的。

