在數學中
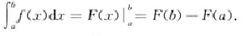牛頓萊布尼茲公式在套用上，積分作用不僅如此，它被大量套用於求和，通俗的說是求曲邊多邊形的面積，這巧妙的求解方法是積分特殊的性質決定的。
一個函式的不定積分（亦稱原函式）指另一族函式，這一族函式的導函式恰為前一函式。
其中：[F(x) + C]' = f(x)
一個實變函式在區間[a,b]上的定積分，是一個實數。它等於該函式的一個原函式在b的值減去在a的值。
因為 ∫*dx= ∫dx=x,所以積分符號 ∫與微分符號d相乘時可以抵消。
基本積分表：
(1) ∫0d x= C
(2)∫ad x=a x+ C
(3) ∫d x/ x=ln| x|+ C
(4)∫ x^md x=(1/(m+1)) x^(m+1)+ C( m≠-1， x>0)
(5)∫a^ xd x=(1/lna)a^ x+C( a>0, a≠1),特別地∫e^ xd x=e^ x+ C
(6) ∫cos xd x=sin x+ C
(7) ∫sin xd x=-cos x+ C
(8) ∫sec xd x=tan x+ C
(9) ∫csc xd x=-cot x+ C
(10) ∫sec xtan xd x=sec x+ C
(11) ∫csc xcot xd x=-csc x+ C
(12)∫d x/sqrt(1- x²)=arcsin x+ C
(13)∫d x/(1+ x²)=arctan x+ C
(14)∫d x/sqrt(1+ x²)=arsh x+ C=ln( x+sqrt( x²+1))+ C
(15)∫d x/sqrt( x²-1)=(|x|/x)arch|x|+ C=ln| x+sqrt( x²-1)|+ C
(16)∫d x/(1- x²) =(1/2)ln|(1+ x)/(1- x)|+ C
在英語中
[∫]在英語中是一種音標，常用於字母組 sh 。
