簡介
sinx的導數是cosx (其中x為變數）
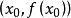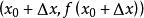SinX的導數
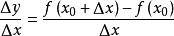SinX的導數
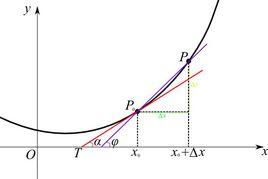
SinX的導數曲線上有兩點 ， 當△x趨向0時, 極限存在，稱y=f(x)在x0處可導，並把這個極限稱f(x)在X1處的導數,這是可導的定義．
正弦函式
正弦函式 sin(x)的導數(導函式)是餘弦 cos(x)，推算過程： 前提是兩個東西要先記住:
sin A - sin B = 2 *(cos (（A + B）/2)) * (sin (（A - B）/2))
以及
lim q -> 0 (sin（q）)/q = 1
先要證明
lim (sin θ)/θ = 1
θ→0
然後
sinθ-sinφ=2cos(θ/2+φ/2)sin(θ/2-φ/2) （三角函式和差化積公式）
y = f(x) = sin(x)
dy/dx
=lim[f(x+Δx)-f(x)]/Δx
Δx→0
=lim[sin(x+Δx)-sin(x)]/Δx
Δx→0
=lim{2cos[(2x+Δx)/2]sin[(x+Δx-x)/2]}/Δx
Δx→0
=lim2[cos(x+Δx/2)sin(Δx/2]/Δx
Δx→0
=lim[cos(x+Δx/2)sin(Δx/2]/(Δx/2)
Δx→0
=cosx × 1
=cosx
求sin x與cos x的 n 階導數：
(sinx)'=cosx
(sinx)''=(cosx)'=-sinx=sin(x+2pi/2)
(sinx)'''=(-sinx)'=-cosx=sin(x+3pi/2)
(sinx)^(4)=(-cosx)'=sinx=sin(x+4pi/2)
…………………………經過歸納得到
(sinx)^(n)=…………………=sin(x+nπ/2)
定義餘弦函式也是同樣的。
證明
根據導數定義
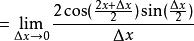SinX的導數由於
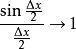SinX的導數所以
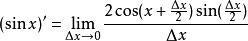SinX的導數
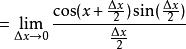SinX的導數
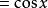SinX的導數證畢.
