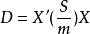霍特林T平方分布1. 定義：一個隨機變數D服從自由度為(p,m)的霍特林T平方分布等價於 ，
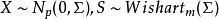霍特林T平方分布, 並且X和S相互獨立。
2. 解釋：
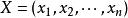霍特林T平方分布
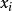霍特林T平方分布
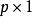霍特林T平方分布 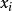霍特林T平方分布(1) 定義中的 , 其中 是 的向量，每個 相互獨立並且服從p元常態分配，
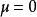霍特林T平方分布
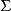霍特林T平方分布均數: , 公共協方差矩陣為 。
霍特林T平方分布(2) 定義中的S服從自由度為m的威希特分布(Wishart distribution)，公共協方差矩陣為 。
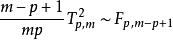霍特林T平方分布3. 與F分布的關係：
4. 假設檢驗
(1) 檢驗一個多元常態分配的平均數：置信區間
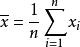霍特林T平方分布首先計算出樣本平均數：
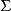霍特林T平方分布
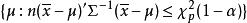霍特林T平方分布(a) 如果已知 ，
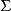霍特林T平方分布
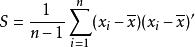霍特林T平方分布
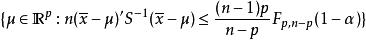霍特林T平方分布(b)如果未知 ， ， 。
(2) 檢驗兩個多元常態分配的平均數：
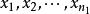霍特林T平方分布
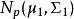霍特林T平方分布
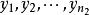霍特林T平方分布
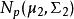霍特林T平方分布
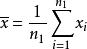霍特林T平方分布
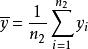霍特林T平方分布
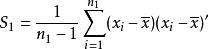霍特林T平方分布
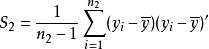霍特林T平方分布隨機變數 服從 , 隨機變數 服從 。 , , ,。
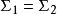霍特林T平方分布
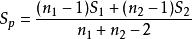霍特林T平方分布(a) 如果兩個樣本的協方差矩陣相同, 定義。
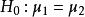霍特林T平方分布
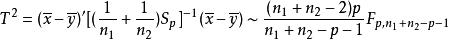霍特林T平方分布統計量：
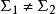霍特林T平方分布
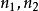霍特林T平方分布(b) 如果兩個樣本的協方差矩陣不同, 隨著的增長，統計量服從卡方分布。
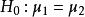霍特林T平方分布
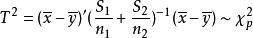霍特林T平方分布統計量：
(3) 檢驗K個多元常態分配的平均數：
需要(MANOVA: Multivariate analysis of variance)。這個檢驗叫做Wilks' lambda test.
5. 單變數假設檢驗的不足
霍特林T平方分布(1) 一類錯誤的發生率高於實際的
(2)多元假設檢驗有更強的能力檢測出樣本間的區別，尤其是在某些情況下，當單變數假設檢驗無法拒絕0假設時，多元假設檢驗可以拒絕0假設
