公式
用數學術語就是:
 需求價格彈性
需求價格彈性需求彈性 = 需求量變化的百分比÷價格變化的百分比
即需求量變化的百分比除以價格變化的百分比。需求的價格彈性實際上是負數;也就是說,由於需求規律的作用,價格和需求量是呈相反方向變化的,價格下跌,需求量增加;價格上升,需求量減少。因此,需求量和價格的相對變化量符號相反,所以需求價格彈性係數總是負數。由於他的符號始終不變,為了簡單起見,習慣上將需求看做為一個正數,因為我們知道它是個負數。
基本類型
當 需求量變動百分數大於價格變動百分數,需求彈性係數大於1時,叫做需求富有彈性或高彈性;
當 需求量變動百分數等於價格變動百分數,需求彈性係數等於1時,叫做需求單一彈性;
當 需求量變動百分數小於價格變動百分數,需求彈性係數小於1時,叫做需求缺乏彈性或低彈性。
含義
彈性理論的目的在於說明價格變化 比率與 需求量(或 供給量)的變動比率之間的關係。
需求彈性的概念:影響 需求量的某因素(自變數)的值每變動百分之一,所引起 需求量變化的 百分率。即:
一、需求價格彈性
1、定義
價格的值每變動百分之一而引起 需求量變化的 百分率。通常,用價格變動的 百分率引起 需求量變化的百分率來表示。這兩個 百分率的比值,稱為 彈性係數,記為Ep,即:
Ed的性質
(1) Ed的 數值,不隨選用的計量單位而變化。
(2) Ed的 數值,可能為正數、負數、等於0或等於1。依賴於有關兩個變數是同方向變化,還是反方向變化。
Ed為正還是為負,所表示的僅僅是有關變數變化的方向性關係,而Ep的 絕對值的大小則表示了變化程度的大小。有時,為了便於比較彈性值的大小,在等式右端添加一個負號,使其成為正值。通常用 絕對值的大小來表示價格變動對 需求量變動的影響程度。當我們說,某產品的需求價格彈性大,即指其 絕對值大。
(3) Ed的 數值,隨 商品的不同而不同。即使在同一種 商品的一條既定的需求 曲線上,也隨價格不同而不同。
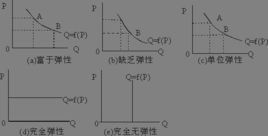
Ed的變動範圍
(1) Ed=1(單位需求價格彈性)。說明 需求量變動幅度與價格變動幅度相同。即價格每提高1%, 需求量相應地降低1%。反之則反是。
需求曲線特點:等軸雙曲線或正雙曲線。需求方程:PQ=K( 常數)。
(2) 1<Ed<∝(需求富有彈性)。說明 需求量變動幅度大於價格變動幅度(ΔP/P<ΔQ/Q=。即價格每變動1%, 需求量變動大於1%。
需求曲線特點:比較平坦( 斜率較小)。
(3) 0<Ed<1(需求缺乏彈性)。 說明 需求量變動幅度小於價格變動幅度(ΔP/P>ΔQ/Q)。即價格每變動1%, 需求量變動的 百分率將小於1%。
需求曲線特點:較陡( 斜率較大)。
(4) Ed→0(需求完全無彈性)。此時,意味著ΔQ/Q=0。在這種情況下,需求狀況具有如下特點: 需求量不隨價格的變動而變動。需求函式的形式為:Q=K(任意既定 常數)。在二維空間圖上, 需求曲線是一條垂直於橫 坐標的直線,在橫坐標上截距等於K(=Q0)。這表示不管價格怎樣變動, 需求量總是固定不變。即不管ΔP的 數值如何,ΔQ之值總是為零。這種情況是罕見的。
(5) Ed→∝(需求完全有彈性),此時,ΔP/P→0。在這種情況下,需求狀況具有如下特點:在既定價格之下, 需求量可以任意變動。需求函式的形式為:P=K( 常數)。 需求曲線將是一條與橫 坐標平行的直線,與橫坐標的距離,既定為 常數K(=P0)。這種情況也是罕見的。在現實生活中,自由市場上某些同質的產品,由於競爭的結果,都按同一價格出售,基本屬於這類 需求曲線的例子。
需求價格彈性的數學計算
(1) 一般計算法。計算公式為:
根據上述公式計算的彈性值,雖然ΔQ與ΔP的 數值相同,但據以計算價格變動 百分率(ΔP/P)的P和據以計算 需求變動百分率(ΔQ/Q)的Q,在兩種場合(價格上升、價格下降)各不相同。就是說,雖然價格變動的 絕對值與由此引起的 需求量變動的絕對值相同,只是由於計算的基礎不同,所以得出的彈性值也就不同。
為解決上述問題,可採用另一種計算方法。即把計算價格變動的 百分率所用價格用變動前後兩個價格的算術平均數來代替,而計算 需求變動百分率的 需求量則用變動前後兩個需求量的算術平均數來代替。這樣,不管從價格向下降落還是從價格向上提高出發,據以計算變動 百分率的P和Q的 數值相同,於是得出 彈性係數的另一種計算方法,即求 弧彈性。
(2) 求 弧彈性。 求 弧彈性,即要計算 需求曲線上某兩點之間一段弧的平均彈性。因而稱之為弧 彈性係數。如果不知道 需求曲線方程,只知道需求曲線上兩點的 坐標(更多的屬於這種情況)。只要 假定在兩次數據觀察之間,所有別的影響需求的變數保持不變,則可由上式求得弧 彈性係數。
需要指出:要使價格向下與價格向上時的Ep一致,取價格的小者,數量的小者為基數,也可得到Ep值相同的結果。
(3) 求 點彈性 若需求函式為已知,即可根據上式求出任一價格下的點 彈性係數。
例:設某 商品的需求函式為:Q= 30-5P
∵dQ/dP=-5
∴EP=|-5×P/Q|=5P/(30-5P)
這表明 點彈性EP是價格P的函式。
若P=2,則Q=20→EP=0.5
若P=3,則Q=15→EP=1.0
若P=4,則Q=10→EP=2.0
結論:對一個既定的需求函式,在不同的價格之下會有不同的彈性值。
圖2-5中,B為中點,當BC=AB時,EP=1;
當BCB→C時,因BC→0,所以EP→0;
當BC>AB時,EP>1,位於B點左上方任一點的彈性係數的絕對值大於1,而且距A點越近的彈性係數,其絕對值越大;
當B→A時,因BA→0,所以EP→∝。
價格彈性與需求曲線的斜率是兩個不同的概念,但二者有所聯繫。價格彈性與需求曲線的斜率ΔP/ΔQ成反比,與P/Q的值成正比。因此,如果需求曲線是一條<a>直線,儘管這條直線上各點的 斜率不變,但由於P/Q的值是變動的,所以這條直線上的價格彈性也是變動的。但如果其它條件相同,那么,平坦的需求曲線彈性大,陡的需求曲線彈性小。
(4)需求價格彈性的幾何求法
當 需求曲線為直線時,可以證明B點的 點彈性為BC/AB。
已知價格彈性的公式為:
ΔQ=LM=GH;Q=OL;
ΔP=EF=BG;P=OE。
代入①式得:
GH OE
Ep= —— · —— ②
BG OL
∵ΔBGH~ΔBLC,BL=OE
GH LC LC
∴——=——=——
BG BL OE
代入②式得:
LC OE LC BC
Ep=—— · ——=——=——
OE OL OL AB
∵ΔAEB~ΔBLC (BE=OL)
LC BC LC BC
∴——=—— ——=——
BE AB OL AB
5、Ep與TR之間的關係
P
Ep>1
Ep=1
Ep<1
P上升
TR減少
TR不變 TR增加
P下降
TR增加
TR不變 TR減少
Ep>1時,P、TR反方向變動;
Ep<1時,P、TR同方向變動。