程式
 雷米茲演算法
雷米茲演算法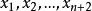 雷米茲演算法
雷米茲演算法雷米茲算法由一函式f開始,欲近似一集合X,且在近似的區間上工有 個取樣點 , 通常Chebyshev nodes可映射至該區間,步驟如下:
解線性系統之等式
1.解線性系統之等式
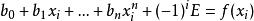 雷米茲演算法
雷米茲演算法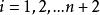 雷米茲演算法
雷米茲演算法(其中 ),
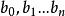 雷米茲演算法
雷米茲演算法對於未知的 及E。
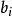 雷米茲演算法
雷米茲演算法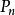 雷米茲演算法
雷米茲演算法使用 作為多項式 的係數。
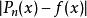 雷米茲演算法
雷米茲演算法找出集合M,為 之區域極大錯誤點。
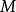 雷米茲演算法
雷米茲演算法 雷米茲演算法
雷米茲演算法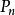 雷米茲演算法
雷米茲演算法若在 之中的所有 都是相同大小,僅正負號不同的話,則 為極小化極大近似之多項式。若否,則M取代X並重複上述步驟。
此結果稱為最佳近似多項式、切比雪夫近似、或最小化最大近似。
初始化選擇
由於切比雪夫節點在多項式插值理論中所扮演的腳色,故通常選擇其為初始近似的方法。由拉格朗日插值法 L( f) 初始化一函式 f之最佳化問題,可以證明此初始近似之邊界限制為:
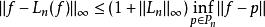 雷米茲演算法
雷米茲演算法其中節點 ( t, ..., t) 之拉格朗日插值法運算元的常數為
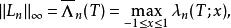 雷米茲演算法
雷米茲演算法T為切比雪夫多項式的零點,而
 雷米茲演算法
雷米茲演算法對提供次最佳之切比雪夫節點來說,其漸進線為
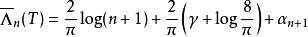 雷米茲演算法
雷米茲演算法( γ為歐拉-馬歇羅尼常數),
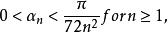 雷米茲演算法
雷米茲演算法而上界為
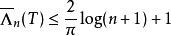 雷米茲演算法
雷米茲演算法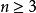 雷米茲演算法
雷米茲演算法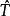 雷米茲演算法
雷米茲演算法Lev Brutman 計算出對 的邊界,而 為切比雪夫多項式之零點
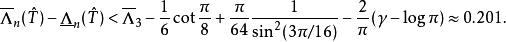 雷米茲演算法
雷米茲演算法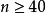 雷米茲演算法
雷米茲演算法Rüdiger Günttner由對 之較粗略的估算計算出
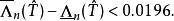 雷米茲演算法
雷米茲演算法細節討論
在此將提供先前簡述步驟的詳細內容 ,在這個章節令指數 i從 0 跑到 n+1.
步驟 1:給定 , 求 n+2 條等式之線性系統之解
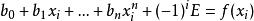 雷米茲演算法
雷米茲演算法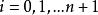 雷米茲演算法
雷米茲演算法(其中),
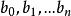 雷米茲演算法
雷米茲演算法對於未知的 和 E.
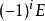 雷米茲演算法
雷米茲演算法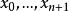 雷米茲演算法
雷米茲演算法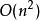 雷米茲演算法
雷米茲演算法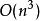 雷米茲演算法
雷米茲演算法可以很清楚地觀察到,在這個式子裡 若要成立,只有在節點 為 排序的情況下才能達到,無論是嚴格遞增或遞減。這樣一來這個線性系統便有唯一解。(廣為人知的,並非每個線性系統都可以求解)。 此外,求解之複雜度最少為 ,而一個從函式庫求解的標準計算器需要的複雜度,在此有一簡單證明:
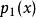 雷米茲演算法
雷米茲演算法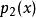 雷米茲演算法
雷米茲演算法計算前 n+1個節點之{\displaystyle f(x)}標準 n階插值, 以及對於{\displaystyle (-1)^{i}}之標準 n階插值
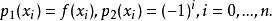 雷米茲演算法
雷米茲演算法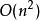 雷米茲演算法
雷米茲演算法至此,需要次數值運算。
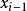 雷米茲演算法
雷米茲演算法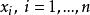 雷米茲演算法
雷米茲演算法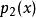 雷米茲演算法
雷米茲演算法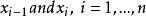 雷米茲演算法
雷米茲演算法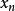 雷米茲演算法
雷米茲演算法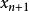 雷米茲演算法
雷米茲演算法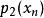 雷米茲演算法
雷米茲演算法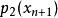 雷米茲演算法
雷米茲演算法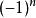 雷米茲演算法
雷米茲演算法在 與 之間,多項式 有其 i-階 零點zero between,因此在與之間無任何零點,意即與正負號相同。
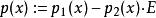 雷米茲演算法
雷米茲演算法線性組合亦為一 n次多項式
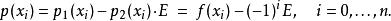 雷米茲演算法
雷米茲演算法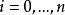 雷米茲演算法
雷米茲演算法選擇任何 E,對 ,下列式子與上述等式相同:
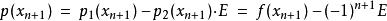 雷米茲演算法
雷米茲演算法解 E得:
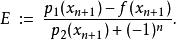 雷米茲演算法
雷米茲演算法如前述所提及,上式分母之兩項有相同正負號,因此
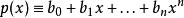 雷米茲演算法
雷米茲演算法是完整定義的。
給定 n+2 階節點,其誤差為正負輪流:
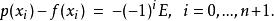 雷米茲演算法
雷米茲演算法de La Vallée Poussin理論說明在這種形況下,沒有誤差少於 E之 n次多項式存在。
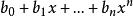 雷米茲演算法
雷米茲演算法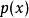 雷米茲演算法
雷米茲演算法步驟 2把多項式表示由 轉為.
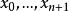 雷米茲演算法
雷米茲演算法步驟 3依照以下所述改善輸入節點 的誤差{\displaystyle \pm E}。
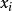 雷米茲演算法
雷米茲演算法 雷米茲演算法
雷米茲演算法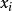 雷米茲演算法
雷米茲演算法在每個 P-領域,現在的節點 將被區域最大 取代,同樣在每個 N-領域, 將被區域最小取代, 在這部分並不要求高精確律。
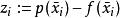 雷米茲演算法
雷米茲演算法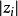 雷米茲演算法
雷米茲演算法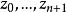 雷米茲演算法
雷米茲演算法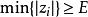 雷米茲演算法
雷米茲演算法令, 其大小 皆大於或等於 E。 de La Vallée Poussin理論及其證明也可以套用至, 而使此 n次多項式有最小可能誤差的新下界為。
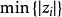 雷米茲演算法
雷米茲演算法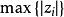 雷米茲演算法
雷米茲演算法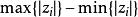 雷米茲演算法
雷米茲演算法步驟 4:分別以
與為新的上下界,此疊代算法的終止條件為: 重複上述步驟直到足夠小且不再遞減。變異
有時候在最大絕對差異點的附近,會有複數個點同時被取代。
有時候相對誤差會被用來衡量函式與其近似的差異,特別是在電腦上用浮點數做運算的函式。
