 費氏數列
費氏數列費氏數列,又譯為“費波那契數列”或“斐波那契序列”;中世紀的義大利數學家費波那契(Leonardo Fibonacci,西元1170-1250年)發現了這樣的一個數列: 1、1、2、3、5、8、13、……;後人稱之為費氏數列,並且對其性質加以研究與套用、發揚光大。
簡介
 費氏數列
費氏數列費氏數列是是由一連串的數字所組成的(假設為a 1 、a 2 、a 3 ……a n-1 、a n ),而且這串數字之間具有一定的規則,就是:每一個數字必須是前兩個數字的和( a n = a n-1 + a n-2 )。 每一個數字必須是前兩個數字的和( a n = a n-1 + a n-2 )。
後人也發現費氏數列有一些耐人尋味的有趣性質,當費氏數列一直算到很大或無限大的時候( 也就是n值無限大時),後項除以前項的極限是黃金分割的值;而數學家也發現在大自然中,可以費氏數列來描述某些植物的生長規則,例如雛菊的花瓣的生長數目。後人也發現費氏數列有一些耐人尋味的有趣性質,例如:當費氏數列一直算到很大或無限大的時候(也就是n值無限大時),後項除以前項的極限是黃金分割的值;而數學家也發現在大自然中,可以費氏數列來描述某些植物的生長規則,例如雛菊的花瓣的生長數目。
性質
 費氏數列
費氏數列性質一:
費氏數列的通項費氏數列的通項
性質二:
a n =a nm x a m+1 + a nm-1 x a m a n =a nm xa m+1 + a nm-1 xa m
性質三:
a n和a n-1互質 a n和a n-1互質
性質四:
若 m|n 則a m |a n若m|n則a m |a n
性質五:
若 m和n互質 則a m和a n互質若m和n互質則a m和a n互質
性質六:
當m,n有最大公因數k時, a m ,a n有最大公因數a k當m,n有最大公因數k時, a m ,a n有最大公因數a k
解決問題
 費氏數列
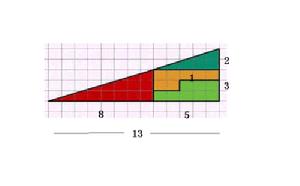
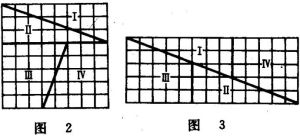
費氏數列一位魔術師拿著一塊邊長為8英尺的正方形地毯,對他的地毯匠朋友說:“請您把這塊地毯分成四小塊,再把它們縫成一塊長13英尺、寬5英尺的長方形地毯。”這位匠師對魔術師算術之差深感驚異,因為8英尺的正方形地毯面積是64平方英尺,如何能夠拼出65平方英尺的地毯?兩者之間面積相差達一平方英尺呢!可是魔術師做到了。他讓匠師用圖2和圖3的辦法達到了他的目的!
真是不可思議!那神奇的1平方英尺究竟從哪裡跑出來的呢?這就是費氏數列(也稱作斐波那契數列)的奧妙所在。
斐波那契數列用文字來說就是,斐波那契數列由0和1開始,之後的斐波那契數(費氏數)就由之前的兩數相加。頭幾個斐波那契數是(OEIS A000045):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,………………
特別指出:0不是第一項,而是第零項。這個數列從第三項開始,每一項都等於前兩項之和。它的通項公式為:(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}(又叫“比內公式”,是用無理數表示有理數的一個範例。)“√5表示根號5
很有趣的是:這樣一個完全是自然數的數列,通項公式居然是用無理數來表達的。隨著數列項數的增加,前一項與後一項之比越逼近黃金分割0.6180339887……
讓我們再回到上文魔術師拼地毯的遊戲:為什麼64=65?其實這是利用了斐波那契數列的這個性質:5、8、13正是數列中相鄰的三項,事實上前後兩塊的面積確實差1,只不過後面那個圖中有一條細長的狹縫,一般人不容易注意到!
1150年印度數學家戈帕拉(Gopala)和金月在研究箱子包裝物件長寬剛好為1和2的可行方法數目時,首先描述了這個數列。在西方,最先研究這個數列的人是義大利比薩的李奧納多·斐波那契,他描述兔子生長的數目時用上了這個數列。
第一個月有一對剛誕生的兔子
第兩個月之後它們可以生育
每月每對可生育的兔子會誕生下一對新兔子
兔子永不死去
假設在n月有新生及可生育的兔子總共a對,n+1月就總共有b對。在n+2月必定總共有a+b對:因為在n+2月的時候,所有在n月就已存在的a對兔子皆已可以生育並誕下a對後代;同時在前一月(n+1月)之b對兔子中,在當月屬於新誕生的兔子尚不能生育。
 費氏數列
費氏數列斐波那契數列又因數學家列昂納多·斐波那契以兔子繁殖為例子而引入,故又稱為“兔子數列”。
需要一段“休息”時間,供自身生長,而後才能萌發新枝。所以,一株樹苗在一段間隔,例如一年,以後長出一條新枝;第二年新枝“休息”,老枝依舊萌發;此後,老枝與“休息”過一年的枝同時萌發,當年生的新枝則次年“休息”。這樣,一株樹木各個年份的枝椏數,便構成斐波那契數列。這個規律,就是生物學上著名的“魯德維格定律”。
另外,觀察延齡草,野玫瑰,南美血根草,大波斯菊,金鳳花,耬斗菜,百合花,蝴蝶花的花瓣,可以發現它們花瓣數目具有斐波那契數:3,5,8,13,21……
自然界中到處可見費氏數列的蹤跡。樹技上的分枝數,多數花的瓣數都是費氏數:火鶴 1、百合 3,梅花 5,桔梗常為 8,金盞花 13,…等等。費氏數列也出現在松果上。一片片的鱗片在整粒松果上順著兩組螺線排列:一組呈順時針鏇轉,另一組呈反時針。仔細瞧瞧,順時針螺線的排列數目是 8,反時針方向則為 13,而另一組常出現的數字是“5和8”。
向日葵也是一樣,常見的螺線數目為“34和55”,較大的向日葵的螺線數目則為“89和144”,更大的甚至還有“144和233”。這些全都是費氏數列中相鄰兩項的數值。
植物是以種子和嫩芽開始生長;種子發芽後,很多細根會長出來,並且向地底下生長,而嫩芽則是迎向陽光。
如果用顯微鏡觀察新芽的頂端,可以看到所有植物的主要征貌的生長過程——包括葉子、花瓣、萼片、小花(floret)等等。在頂端的中央,有一個圓形的組織稱為“頂尖”(apex);而在頂尖的周圍,則有微小隆起物一個接一個的形成,這些隆起則稱為“原基”(primordium)。
生長時,每一個原基自頂尖移開(頂尖從隆起處向外生長,新的原基則在原地);最後,這些隆起原基會長成葉子、花瓣、萼片等等。每個原基都希望生成的花、蕊、或葉片等等,之後能夠獲得最大的生長空間。例如葉片希望得到充足的陽光,根部則希望得到充足的水份,花瓣或花蕊則希望充份地自我展現好吸引昆蟲來傳粉。因此,原基與原基隔得相當開,由於較早產生的原基移開的較遠,所以你可以從它與頂尖之間的距離,來推斷出現的先後次序。另人驚奇的是,我們若依照原基的生成時間順序描出原基的位置,便可畫出一條卷繞得非常緊的螺線——稱為“生成螺線”(generative spiral)。
 費氏數列
費氏數列前面提到的左右鏇螺線,雖然能夠明顯到讓人一眼看出(植物學家稱之為“斜列線”,但那並不是植物的原基生長模式的實際表征;就某種程度而言,這些螺線只是視學上的錯覺。人的眼睛之所以能分辨出斜列線,是因為斜列線是由相鄰的原基所形成。
晶體學先驅布拉菲兄弟(Auguste and Louise Bravais)發現原基沿生成螺線交錯排列的數學規則。他們量測相鄰兩原基之間的角度,發現量得的各個角度非常相近;這些角的共同值就稱為“發散角”。
想像從原基的中心各畫一條直線連到頂尖的中心,然後測量這兩條線的夾角。他們發現發散角往往非常接近 137.5 度(或 222.5 度,如果從另一邊量起),也就是 ――“黃金角”。如果我們將一個圓分成兩個弧,而兩個弧的長度比為黃金比例,小弧的圓心角也就是黃金角。
