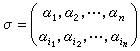相關性質
定理1 不相連輪換相乘時可以交換
定理2 每個(非輪換)的置換都可表為不相連輪換之積;每個輪換都可表為對換之積,因此,每個置換都可表為對換之積
定理3 每個置換表成對換的乘積時,其對換個數的奇偶性不變
凱萊定理
任一有限群都與其元素的一個置換群同構。
區及軌道 設G是Ω上一個置換群,墹是Ω的一個子集,g是G中任一元素,用墹g表示墹在g下的像集
 公式 公式 |
。若對於G中任一元素 g都有墹g=墹,或
 公式 公式 |
,則稱墹是一個區。空集═以及Ω都是區,稱為平凡區。其餘的區稱為非平凡區。兩個區的交仍是區。
若對G中任一元素g,都有墹g=墹,則稱 墹是G的一個不變區。Ω及═都是不變區。不變區的交仍是不變區。
設墹是G的一個不變區,如果對墹中任意兩個點α、β都有G中一個元素g使得αg=β,那么墹稱為G 的一個軌道(或傳遞集)。如果墹是G 的一個軌道,那么,任取墹中一個點α,都有
 公式 公式 |
。而且,G 的任一個軌道都可這樣得到。如果墹及Γ是G 的兩個軌道,那么墹=Г 或墹∩Г=═。因此,Ω分成G 的一些兩兩不交的軌道之並。軌道中元素的個數稱為軌道的長度。
穩定子群
設G是一個n元置換群,作用於Ω上。取定Ω中一個點α
 公式 公式 |
,是G 的一個子群,稱為G 對α 的穩定子群。如果
 公式 公式 |
,並設
 公式 公式 |
(通常取恆等置換作為g1),那么
 公式 公式 |
。因此,|G|=|Gα||αG|,所以G 的軌道的長度一定能整除G 的階。
如果對任一α∈Ω,都有Gα={e},則稱G是半正則群。此時,G的任一軌道長都等於|G|。
穩定子群的概念還可以推廣到多個點的情形。取定Ω中k個點α1,α2,…,αk,則是G的一個子群,稱為G對α1,α2,…,αk的穩定子群。顯然有。
正文
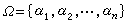 置換群
置換群由置換組成的群。n 元集合
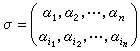 置換群
置換群到它自身的一個一一映射,稱為Ω上的一個置換或 n元置換。Ω上的置換σ可表為
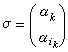 置換群
置換群或簡記為
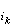 置換群
置換群,其中i1,i2,…,in是1,2,…,n的一個排列,α
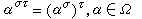 置換群
置換群是 αk在置換σ下的像。有時也把α 在σ下的像記為α。根據映射的乘法可以定義Ω上任意兩個置換σ與τ的乘積στ為
。對於這樣定義的運算,Ω上全體置換所組成的集合S成一個群,稱為Ω上的對稱群或n元對稱群,簡稱對稱群,其階為 n!。對稱群的子群稱為Ω上的置換群或簡稱置換群。當Ω={1,2,…,n}時把S 記為Sn。較置換群更為一般的概念,有所謂的作用。
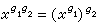 置換群
置換群作用G是一個群,Ω是一個非空集合。G中每個元素g都對應Ω的一個映射:x→x,x∈Ω,若滿足:①
;②x=x(e是G的單位元素),則稱G作用於Ω上。G作用於Ω上的充分必要條件是,G同態於Ω上的一個置換群。
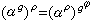 置換群
置換群設G是Ω上的一個置換群,H是Γ上的一個置換群。如果存在Ω到Γ上的一個一一對應ρ,以及G到H上的一個一一對應φ,使得對Ω中任一個點α及G中任一個置換g都有
,那么G與H 稱為置換同構的。兩個置換同構的置換群一定是同構的。但是同構的置換群不一定是置換同構的。
如果 Ω與Γ都是n元集合,那么S與Sг是置換同構的。因此,n元對稱群都與Sn置換同構。
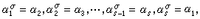 置換群
置換群設σ是Ω上一個置換,若Ω中一些點α1,α2,…,αs使得
而σ保持Ω中其餘的點不動,那么σ稱為一個輪換,記作(α1,α2,…,αs)。若兩個輪換沒有公共的變動點,則稱這兩個輪換是不相交的。每一個置換都可表為不相交輪換的乘積,稱為置換的輪換表示法,而且除表示式中輪換的次序以外,置換的輪換表示法是惟一的。
兩個點的輪換稱為對換。任一置換都可表為一些對換的乘積,表示法不是惟一的,但是表示式中對換個數的奇偶是惟一確定的。若σ可表成偶數個對換的乘積,則稱σ為偶置換。若σ可表成奇數個對換的乘積,則稱σ為奇置換。
S中全部偶置換組成S的一個正規子群,稱為n元交錯群,簡稱交錯群,記作A。Sn的交錯子群記作An。n元交錯群都與An置換同構。當n≥2時,An的階為n!/2。當n≠4時,An是單群,這是一類很重要的有限單群。
置換群是有限群的一類重要例子,有限群的研究是從置換群開始的。置換群的重要性還在於下述事實。
凱萊定理任一有限群都與其元素的一個置換群同構。
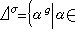 置換群
置換群區及軌道 設G是Ω上一個置換群,墹是Ω的一個子集,g是G中任一元素,用墹表示墹在g下的像集
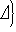 置換群
置換群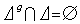 置換群
置換群。若對於G中任一元素 g都有墹=墹,或
,則稱墹是一個區。空集═以及Ω都是區,稱為平凡區。其餘的區稱為非平凡區。兩個區的交仍是區。
若對G中任一元素g,都有墹=墹,則稱 墹是G的一個不變區。Ω及═都是不變區。不變區的交仍是不變區。
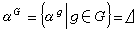 置換群
置換群設墹是G的一個不變區,如果對墹中任意兩個點α、β都有G中一個元素g使得α=β,那么墹稱為G 的一個軌道(或傳遞集)。如果墹是G 的一個軌道,那么,任取墹中一個點α,都有
。而且,G 的任一個軌道都可這樣得到。如果墹及Γ是G 的兩個軌道,那么墹=Г 或墹∩Г=═。因此,Ω分成G 的一些兩兩不交的軌道之並。軌道中元素的個數稱為軌道的長度。
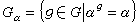 置換群
置換群穩定子群設G是一個n元置換群,作用於Ω上。取定Ω中一個點α,
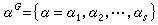 置換群
置換群是G 的一個子群,稱為G 對α 的穩定子群。如果
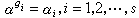 置換群
置換群,並設
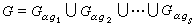 置換群
置換群(通常取恆等置換作為g1),那么
。因此,|G|=|Gα||α|,所以G 的軌道的長度一定能整除G 的階。
如果對任一α∈Ω,都有Gα={e},則稱G是半正則群。此時,G的任一軌道長都等於|G|。
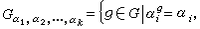 置換群
置換群穩定子群的概念還可以推廣到多個點的情形。取定Ω中k個點α1,α2,…,αk,則
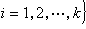 置換群
置換群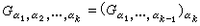 置換群
置換群是G的一個子群,稱為G對α1,α2,…,αk的穩定子群。顯然有
。
傳遞性設G是Ω上一個置換群。若對任意α,β∈Ω,都可找到g∈G,使得α=β,則稱G在Ω上是傳遞的;否則,稱G是非傳遞的。G是傳遞群若且唯若Ω是 G的一個軌道。因此,若G是傳遞群,則|Ω|是|G|的一個因子。若G是傳遞群,且|Ω|=|G|,則稱G是一個正則群。正則群就是傳遞的半正則群。
若在一個非正則傳遞群G中,每個非單位元素最多保持一個文字不變,則G 稱為弗羅貝尼烏斯群。在弗羅貝尼烏斯群G中,沒有不變文字的置換與恆等置換一起構成一個正則群R,R是G 的一個特徵子群。
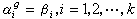 置換群
置換群若對於Ω中任意兩個k元有序點組α1,α2,…,αk及β1,β2,…,βk,都有G中一個置換g使
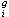 置換群
置換群,則稱G是一個 k重傳遞群或 k傳遞群。k重傳遞群一定是(k-1)重傳遞的。如果k≥2,那么k重傳遞群稱為多重傳遞群,否則稱為單傳遞群。如果G是Ω上一個傳遞群,那么若且唯若Gα在Ω-{α}上(K-1)重傳遞群時,G是k重傳遞的。k重傳遞的n元置換群G 的階可被n(n-1)…(n-k+1)整除。若G 的階恰等於n(n-1)…(n-k+1),則稱G是一個精確 k重傳遞群。此時,對於Ω中任意兩個k元點組α1,α2,…,αk;β1,β2,…,βk,在G中恰有一個g使α
=βi,i=1,2,…,k。
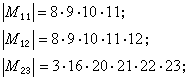 置換群
置換群對稱群Sn是 n重傳遞的,交錯群An是n-2重傳遞的。除去Sn及An外,有無窮多個3重傳遞群,但是只知道4個4重傳遞群,它們是法國數學家 É.L.馬蒂厄在1861年及1873年先後發現的次數分別為11,12,23及24的馬蒂厄群M11,M12,M23,M24,其中M12及M24是5重傳遞的,而且M11是M12的穩定子群,M23是M24的穩定子群,它們的階分別是
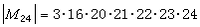 置換群
置換群。
M11及M12都是精確傳遞群。
在1981年有限單群分類的問題解決以後,所有雙重傳遞群已被決定,並且知道沒有傳遞重數大於或等於6的傳遞單群,而交錯群與上述4個馬蒂厄群是僅有的4重傳遞的單置換群。M23的穩定子群是M22,也是一個單群,這5 個馬蒂厄群是最早發現的不屬於有限單群的無窮系列的5個零散單群。
秩設G是Ω上的一個傳遞置換群,α∈Ω,G對α的穩定子群Gα作為Ω上的置換群,其軌道(包括平凡軌道{α})數稱為G的秩。顯然,若且唯若G的秩等於2時,G是雙傳遞的。秩為 3的單傳遞群是一類很重要的單傳遞群,在26個零散單群中,有8個是作為秩是3的置換群構造出來的群。
本原性設G是Ω上一個傳遞群,若G沒有非平凡區, 則稱G是一個本原群,否則稱為非本原群。多重傳遞群一定是本原群,Ω上傳遞群G是本原群的充分必要條件為其穩定子群Gα(α∈Ω)是G的極大子群。如果Ω上一個置換群G是k重傳遞的,並且對k-1個點的穩定子群在其餘的點上是本原的,那么G稱為k重本原的。
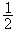 置換群
置換群k重集傳遞性及半傳遞性比k重傳遞性較弱的一個概念是k重集傳遞性。設G是Ω上一個置換群,若對於Ω的任意兩個k元子集Δ、Γ都可找到 G中一個元素g 使得Δ=Γ,則稱G是k重集傳遞的。傳遞性的另一個推廣是所謂半傳遞性,若G的軌道長都相等且大於1,則G稱為半傳遞的,或
重傳遞的。
置換群的一個古老而有意義的問題,是找出全部互不置換同構的置換群。至今,已找出次數小於或等於11的全部置換群。所謂置換群的次數,即這個置換群所有實際變動的點的個數。當12≤n≤15時找出了全部n次傳遞群。而當n較大時,僅對n≤50找出了全部n次本原群。
參考書目
H.Wielandt,Finite Permutation Groups, AcademicPress, New York,1964.
D.Passman,Permutation Groups, Benjamin, New York,1968.
B.Huppert and N.Blackburn,Finite Groups, Vol.3,Springer-Verlag, Berlin,1982.