簡介
球對稱位勢乃是一種只與徑向距離有關的位勢。許多描述宇宙相互作用的基本位勢,像重力勢、電勢,都是球對稱位勢。這條目只講述,在量子力學裡,運動於球對稱位勢中的粒子的量子行為。這量子行為,可以用薛丁格方程表達為
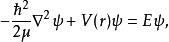 球對稱位勢
球對稱位勢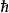 球對稱位勢
球對稱位勢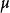 球對稱位勢
球對稱位勢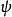 球對稱位勢
球對稱位勢其中, 是普朗克常數, 是粒子的質量, 是粒子的波函式,V是位勢,r是徑向距離,E是能量。
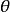 球對稱位勢
球對稱位勢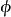 球對稱位勢
球對稱位勢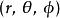 球對稱位勢
球對稱位勢由於球對稱位勢V(r)只與徑向距離有關,與天頂角 、方位角 無關,為了便利分析,可以採用球坐標 來表達這問題的薛丁格方程。然後,使用分離變數法,可以將薛丁格方程分為兩部分,徑向部分與角部分。
薛丁格方程
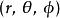 球對稱位勢
球對稱位勢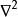 球對稱位勢
球對稱位勢採用球坐標 ,將拉普拉斯運算元 展開:
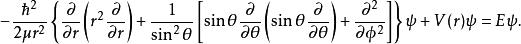 球對稱位勢
球對稱位勢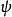 球對稱位勢
球對稱位勢滿足薛丁格方程的本徵函式 的形式為:
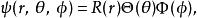 球對稱位勢
球對稱位勢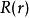 球對稱位勢
球對稱位勢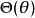 球對稱位勢
球對稱位勢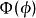 球對稱位勢
球對稱位勢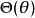 球對稱位勢
球對稱位勢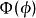 球對稱位勢
球對稱位勢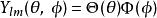 球對稱位勢
球對稱位勢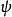 球對稱位勢
球對稱位勢其中, , , ,都是函式。 與 時常會合併為一個函式,稱為球諧函式, 。這樣,本徵函式 的形式變為:
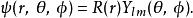 球對稱位勢
球對稱位勢角部分解答
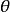 球對稱位勢
球對稱位勢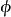 球對稱位勢
球對稱位勢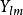 球對稱位勢
球對稱位勢參數為天頂角 、方位角 的球諧函式 ,滿足角部分方程
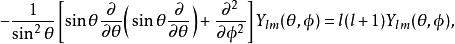 球對稱位勢
球對稱位勢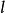 球對稱位勢
球對稱位勢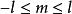 球對稱位勢
球對稱位勢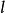 球對稱位勢
球對稱位勢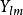 球對稱位勢
球對稱位勢其中,非負整數 是角動量的 角量子數。m(滿足 )是角動量對於z-軸的(量子化的)投影。不同的與m給予不同的球諧函式解答 :
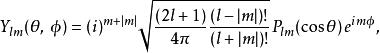 球對稱位勢
球對稱位勢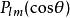 球對稱位勢
球對稱位勢其中,i是虛數單位, 是伴隨勒讓德多項式,用方程定義為
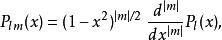 球對稱位勢
球對稱位勢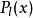 球對稱位勢
球對稱位勢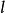 球對稱位勢
球對稱位勢而 是 階勒讓德多項式,可用羅德里格公式表示為
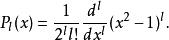 球對稱位勢
球對稱位勢徑向部分解答
將角部分解答代入薛丁格方程,則可得到一個一維的二階微分方程:
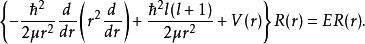 球對稱位勢
球對稱位勢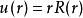 球對稱位勢
球對稱位勢設定函式。代入方程(1)。經過一番繁雜的運算,可以得到
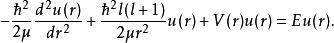 球對稱位勢
球對稱位勢徑向方程變為
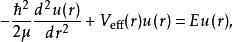 球對稱位勢
球對稱位勢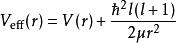 球對稱位勢
球對稱位勢其中,有效位勢。
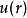 球對稱位勢
球對稱位勢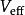 球對稱位勢
球對稱位勢 球對稱位勢
球對稱位勢這正是函式為,有效位勢為的薛丁格方程。徑向距離r的定義域是從0到。新加入有效位勢的項目,稱為離心位勢。
參閱
•自由粒子
•無限深方形阱
•有限深方形阱
•有限位勢壘
•Delta位勢阱
•Delta位勢壘
•有心力
