概念
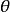 無偏性
無偏性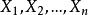 無偏性
無偏性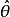 無偏性
無偏性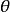 無偏性
無偏性設是總體的未知參數,是總體的一個樣本,是參數的一個估計量,若
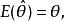 無偏性
無偏性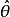 無偏性
無偏性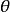 無偏性
無偏性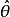 無偏性
無偏性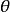 無偏性
無偏性則稱是的一個無偏估計量。若不是的無偏估計量,則稱
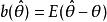 無偏性
無偏性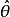 無偏性
無偏性為的偏差。
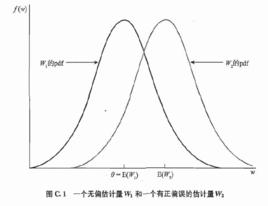
顯然,無偏性的直觀意義是樣本估計量的數值在參數的真值附近擺動。且無系統誤差,即這些估計量的平均值等於未知參數的真值。
證明
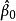 無偏性
無偏性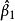 無偏性
無偏性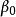 無偏性
無偏性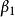 無偏性
無偏性無偏性是指估計量和的數學期望分別等於總體回歸係數的和,即
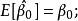 無偏性
無偏性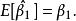 無偏性
無偏性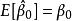 無偏性
無偏性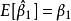 無偏性
無偏性給出和的證明。
證明:
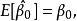 無偏性
無偏性先證
因為
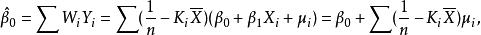 無偏性
無偏性所以
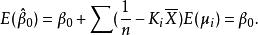 無偏性
無偏性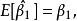 無偏性
無偏性再證明
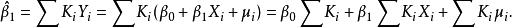 無偏性
無偏性因為
 無偏性
無偏性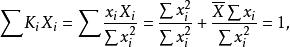 無偏性
無偏性所以
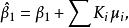 無偏性
無偏性即
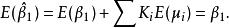 無偏性
無偏性