提出背景
20世紀50年代，美國數學家史蒂芬·科爾·克萊尼提出了正則表達式的三類基本運算：並、連線、克林閉包（又稱星閉包，Kleene星號）。此後學界發現很多時候需要描述一個語言連線1次或以上得到的集合，因此由克林閉包的概念衍生出了正閉包的概念。
定義
正閉包對於語言L，L的正閉包定義為：
性質
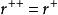正閉包1、冪等性：
digit+的DFA2、結合性：正閉包具有左結合性。
3、優先權：正閉包和克林閉包一樣在正則表達式運算中具有最高優先權。
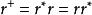正閉包4、由克林閉包推出正閉包：
正閉包5、由正閉包推出克林閉包：
實例
例：由a和b組成且不含有三個連續的b的字元串的正則表達式（All strings of a's and b's that contain no three consecutive b's）。
正閉包答案：
題目來源：《編譯原理與實踐》（英文版）第2章課後題2.1.f題
正閉包
正閉包解析：不含有三個連續的b意味著除了{b}和{bb}這兩種不含有a的情況外，每至多出現2個連續的b後必須出現至少1個a，因此構造出，但這樣寫忽略了以b結尾的情況，因此要在後面連線。這樣再並上b和bb，得到正解。
