套用方面
柯西極限存在準則,又稱柯西收斂準則,是用來判斷某個式子是否收斂的充要條件(不限於數列),主要套用在以下方面:
(1)數列
(2)數項級數
(3)函式
(4)反常積分
(5)函式列和函式項級數
每個方面都對應一個柯西準則,因此下文將按照不同的方面對準則進行說明。
數列
數列的柯西收斂準則
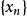 柯西極限存在準則
柯西極限存在準則數列收斂的充分必要條件是:對於任意給定的正數ε,總存在正整數N,使得當m>N,n > N時,且m≠n,有
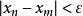 柯西極限存在準則
柯西極限存在準則我們把滿足該條件的{x}稱為柯西序列,那么上述定理可表述成:數列{x}收斂,若且唯若它是一個柯西序列。
該準則的幾何意義表示,數列{x}收斂的充分必要條件是:該數列中的元素隨著序數的增加而愈發靠近,即足夠靠後的任意兩項都無限接近。
證明
必要性
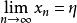 柯西極限存在準則
柯西極限存在準則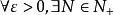 柯西極限存在準則
柯西極限存在準則設,則,當m,n>N時,有
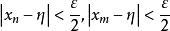 柯西極限存在準則
柯西極限存在準則那么,
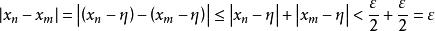 柯西極限存在準則
柯西極限存在準則充分性
由於數列的柯西收斂準則是實數連續性的體現之一,所以用實數公理——戴德金定理證明{x}收斂。
首先證明柯西序列是有界的。根據柯西序列的定義,對任意ε>0,存在正整數N,當m,n>N時,有|x-x|<ε。
於是取m=N+1,則當n>N時,|x-x|<ε。
解得x-ε<x<x+ε,即當n>N時,{x}既有上界又有下界,所以是有界的。
向上述數列中添加{x}的前N項得到{x}本身,則由於前N項都是確定的實數,不會改變{x}的有界性(即使此時{x}的上、下界發生變化)。故對任意正整數n,{x}都是有界的。
其次證明柯西序列收斂。設{x}⊆[a,b],有一個實數集A,A中的任一元素c滿足:區間(-∞,c)中最多有{x}中的有限項(注意用詞“最多”,意味著可以有0項),而{x}中的無限項都落在[c,+∞)。並把A在R中的補集設為B,則:
①由取法可知a∈A,並且顯然b∈B。即A和B都是非空數集。
②A∪B=R。
③根據集合A、B的定義,A中任意元素都小於B中的任意元素。
由戴德金定理得,存在唯一實數η,使η要么是A中的最大值,要么是B中的最小值。
∵η是A和B的分界點
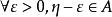 柯西極限存在準則
柯西極限存在準則∴
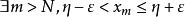 柯西極限存在準則
柯西極限存在準則④由A的定義可知,。
根據已知條件,當m,n>N時,|x-x|<ε
於是x-ε<x<x+ε。聯立④中的不等式,可得到η-2ε<x<η+2ε。
也就是當n>N時,不等式|x-η|<2ε成立
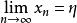 柯西極限存在準則
柯西極限存在準則∴
套用
作為柯西收斂準則的套用之一,我們可以用來證明實數的確界原理。
確界原理:非空有上(下)界數集,必有上(下)確界。
證明:先證非空有上界數集必有上確界。
設S是一個非空有上界的數集,且b是其一個上界。則由S的非空性及實數的有序性可知,必定存在一個實數a,使得a小於S中的某個元素,即a不是S的上界。
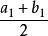 柯西極限存在準則
柯西極限存在準則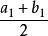 柯西極限存在準則
柯西極限存在準則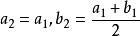 柯西極限存在準則
柯西極限存在準則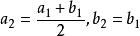 柯西極限存在準則
柯西極限存在準則把閉區間[a,b]二等分,考慮閉區間中點,如果是S的上界,則令;否則令。
 柯西極限存在準則
柯西極限存在準則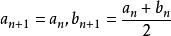 柯西極限存在準則
柯西極限存在準則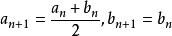 柯西極限存在準則
柯西極限存在準則重複此步驟,即如果某個閉區間中點是S的上界,則令,否則令。這樣一來得到了一系列閉區間,滿足
①a≤a<b≤b
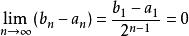 柯西極限存在準則
柯西極限存在準則②
並且由閉區間的構造方式可知,對任意自然數n,a都不是S的上界,而b都是S的上界。
下證{a}、{b}收斂。
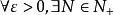 柯西極限存在準則
柯西極限存在準則由極限的定義,根據②可知,,使得當n>N時,|b-a|<ε。
並且對任意正整數n和p,根據①可知,a≤a<b≤b。
於是當n>N時,0≤|a-a|<|b-a|<ε。
令n+p=m,即可得到{a}是一個柯西序列,由柯西收斂準則知{a}收斂。
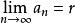 柯西極限存在準則
柯西極限存在準則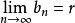 柯西極限存在準則
柯西極限存在準則設,由②得。
下證r是S的上確界。
∵b是S的上界
∴對S中的任一元素x,都有x≤b
由極限的保序性逆定理可知x≤r,即r是S的上界。
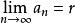 柯西極限存在準則
柯西極限存在準則又取任意r’<r,由及極限保序性可知,存在正整數N,當n>N時,就有a>r'。
∵a不是S的上界
∴r‘不是S的上界
即比r小的數不再是S的上界。根據上確界的定義,r是S的上確界,即非空有上界的數集必有上確界 。
其次,再來證明非空有下界數集必有下確界。
設B是一個非空有下界的數集,A是B的所有下界組成的數集。
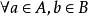 柯西極限存在準則
柯西極限存在準則根據下界的定義,,都有a≤b。換句話說,B中的所有元素都是A的上界,A是一個非空有上界數集。由於已證得非空有上界數集必有上確界,所以A有上確界,記該上確界為r。
下證r也是B的下確界。
顯然r∈A,這是因為如果r∉A,那么r一定是B中的最小值(根據上確界的定義),即對任意B中的元素b,都有r≤b。根據下界的定義,r也是B的一個下界,這樣一來r∈A,與假設矛盾。
又取任意r''>r,所以r''∉A,即比r大的數不再是B的下界。根據下確界的定義,r是B的下確界,即非空有下界數集必有下確界。
數項級數
數項級數的柯西收斂準則
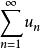 柯西極限存在準則
柯西極限存在準則數項級數 收斂的充要條件是:對於任意給定的正數ε,總存在正整數N,使得當m>n>N時,有
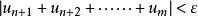 柯西極限存在準則
柯西極限存在準則證明
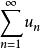 柯西極限存在準則
柯西極限存在準則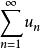 柯西極限存在準則
柯西極限存在準則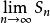 柯西極限存在準則
柯西極限存在準則設數項級數 的部分和為S,根據級數收斂的定義, 收斂若且唯若 收斂。
顯然,對於確定的n來說,S都有唯一一個確定的數值,這樣一來{S}就是一個數列。故考慮用數列的柯西收斂準則來證明。
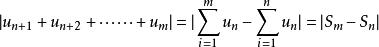 柯西極限存在準則
柯西極限存在準則∵
∴由數列的柯西收斂準則可知,數項級數的柯西收斂準則也成立。
函式
考慮到數列是特殊的函式(即定義域為正整數集),可以猜想,函式的斂散性也應當有類似的結論,這就是接下來要說的函式的柯西收斂準則。
函式的柯西收斂準則
(1)x→x時的準則
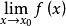 柯西極限存在準則
柯西極限存在準則收斂的充要條件是:對於任意給定的正數ε,總存在正數δ,使得當0<|x-x|<δ,0<|x-x|<δ時,有
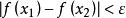 柯西極限存在準則
柯西極限存在準則(2)x→∞時的準則
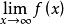 柯西極限存在準則
柯西極限存在準則收斂的充要條件是:對於任意給定的正數ε,總存在正數X,使得當|x|>X,|x|>X時,有
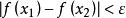 柯西極限存在準則
柯西極限存在準則x、x是f(x)的定義區間上任意兩個實數。
以上準則針對單側極限依然有效。
該準則的充要條件又稱為(函式的)柯西條件,換句話說,函式收斂若且唯若函式滿足柯西條件。
證明
必要性
(1)x→x 時的準則
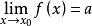 柯西極限存在準則
柯西極限存在準則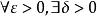 柯西極限存在準則
柯西極限存在準則設 ,則 ,當0<|x-x|<δ,0<|x-x|<δ 時,有
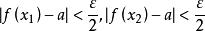 柯西極限存在準則
柯西極限存在準則那么,
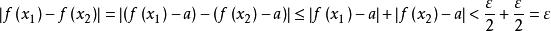 柯西極限存在準則
柯西極限存在準則(2)x→∞ 時的準則
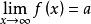 柯西極限存在準則
柯西極限存在準則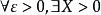 柯西極限存在準則
柯西極限存在準則設 ,則 ,當|x|>X,|x|>X 時,有
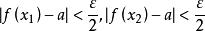 柯西極限存在準則
柯西極限存在準則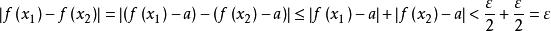 柯西極限存在準則
柯西極限存在準則那么,
充分性
由於函式極限和數列極限可以通過歸結原則聯繫起來,所以要證明函式收斂,可以轉化為證明數列收斂。而數列收斂的柯西準則上面已經證明了,所以把已知條件轉化為求數列極限是證明的重心。
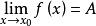 柯西極限存在準則
柯西極限存在準則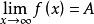 柯西極限存在準則
柯西極限存在準則歸結原則(或稱海涅定理):設f(x)在x的某個去心鄰域(或|x|大於某個正數時)有定義,那么 (或 )的充要條件是,對在x的某個去心鄰域內的 任意收斂於x並且滿足x≠x的數列{x}(或絕對值大於某個正數的 任意發散到無窮大的數列{x}),都有數列{f(x)}收斂到A,即
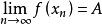 柯西極限存在準則
柯西極限存在準則這個原則在這裡不證明,只需要注意的是定理中的“任意”二字。另外,如果函式極限是單側極限,則相應的任意數列都是單調數列(右極限對應任意單調遞減數列,左極限對應任意單調遞增數列)。
(1)x→x 時的準則
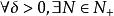 柯西極限存在準則
柯西極限存在準則設{x}是x的某個去心鄰域內的任意收斂到x並且x≠x的數列,由數列極限的定義, (注意這裡的δ就是柯西條件的δ),當m,n>N時,有
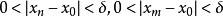 柯西極限存在準則
柯西極限存在準則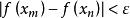 柯西極限存在準則
柯西極限存在準則而由0<|x-x|<δ,0<|x-x|<δ 可知,
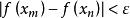 柯西極限存在準則
柯西極限存在準則換句話說,當m,n>N時,有
這也就是數列的柯西收斂準則,由柯西收斂準則可知數列{f(x)}收斂。又因為{x}的任意性,得到任意{x}的極限都相等。於是根據歸結原則,f(x)收斂。
(2)x→∞ 時的準則
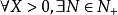 柯西極限存在準則
柯西極限存在準則設{x}是絕對值大於某個正數的任意發散到無窮大的數列,由數列發散到無窮大的定義, (注意這裡的X就是柯西條件的X),當m,n>N時,有
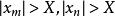 柯西極限存在準則
柯西極限存在準則而由|x|>X,|x|>X 可知,
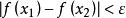 柯西極限存在準則
柯西極限存在準則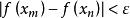 柯西極限存在準則
柯西極限存在準則換句話說,當m,n>N時,有
這也就是數列的柯西收斂準則,由柯西收斂準則可知數列{f(x)}收斂。又因為{x}的任意性,得到任意{x}的極限都相等。於是根據歸結原則,f(x)收斂。
反常積分
反常積分分為兩種,一種是積分區間含有無窮大的反常積分(又叫做無窮限的反常積分),另一種是被積函式為無界函式的反常積分(又叫做無界函式的反常積分、瑕積分)。因此相應的柯西收斂準則有兩種,兩種準則的描述有些區別,但都可以根據函式的柯西收斂準則來證明。
反常積分的柯西收斂準則
(1)無窮限的反常積分
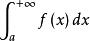 柯西極限存在準則
柯西極限存在準則無窮限的反常積分 收斂的充要條件是,對於任意給定的正數ε,總存在正數X,使得當q>p>X時,有
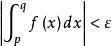 柯西極限存在準則
柯西極限存在準則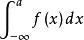 柯西極限存在準則
柯西極限存在準則無窮限的反常積分 收斂的充要條件是,對於任意給定的正數ε,總存在正數X,使得當p<q<-X時,有
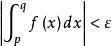 柯西極限存在準則
柯西極限存在準則前提是閉區間[p,q]⊂[a,+∞)(或(-∞,a])。
(2)瑕積分
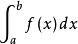 柯西極限存在準則
柯西極限存在準則瑕積分 收斂的充要條件是,對於任意給定的正數ε,總存在正數δ,使得當a<p<q<a+δ時,有
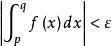 柯西極限存在準則
柯西極限存在準則其中x=a是f(x)的瑕點。
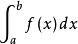 柯西極限存在準則
柯西極限存在準則瑕積分 收斂的充要條件是,對於任意給定的正數ε,總存在正數δ,使得當b-δ<p<q<b時,有
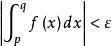 柯西極限存在準則
柯西極限存在準則其中x=b是f(x)的瑕點。
前提是閉區間[p,q]⊂(a,b](或[a,b))。
證明
(1)無窮限的反常積分
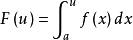 柯西極限存在準則
柯西極限存在準則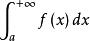 柯西極限存在準則
柯西極限存在準則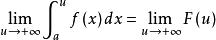 柯西極限存在準則
柯西極限存在準則設 。由無窮限反常積分收斂的定義可知, 收斂,若且唯若 收斂。
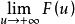 柯西極限存在準則
柯西極限存在準則於是根據函式的柯西收斂準則, 收斂的充要條件是,對於任意ε>0,總存在X>0,使得當p>X,q>X時,有
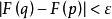 柯西極限存在準則
柯西極限存在準則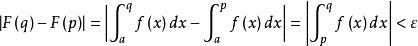 柯西極限存在準則
柯西極限存在準則由定積分的性質可知, 。
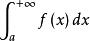 柯西極限存在準則
柯西極限存在準則把上述過程綜合起來,就得到 收斂的充要條件是:對於任意ε>0,總存在X>0,使得當p>X,q>X時,有
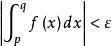 柯西極限存在準則
柯西極限存在準則由此得證無窮限反常積分的柯西收斂準則。
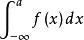 柯西極限存在準則
柯西極限存在準則同理可證。
(2)瑕積分
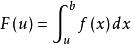 柯西極限存在準則
柯西極限存在準則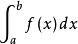 柯西極限存在準則
柯西極限存在準則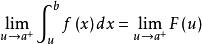 柯西極限存在準則
柯西極限存在準則設 。由瑕積分收斂的定義可知, 收斂(x=a是瑕點),若且唯若 收斂。
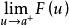 柯西極限存在準則
柯西極限存在準則於是根據函式的柯西收斂準則, 收斂的充要條件是,對於任意給定的正數ε,總存在正數δ,使得當0<p-a<δ,0<q-a<δ時,有
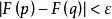 柯西極限存在準則
柯西極限存在準則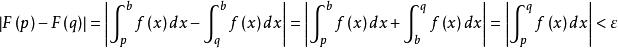 柯西極限存在準則
柯西極限存在準則由定積分的性質可知, 。
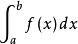 柯西極限存在準則
柯西極限存在準則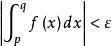 柯西極限存在準則
柯西極限存在準則把上述過程綜合起來,就得到 (x=a是瑕點)收斂的充要條件是,對於任意給定的正數ε,總存在正數δ,使得當0<p-a<δ,0<q-a<δ時,有
但是,0<p-a<δ,0<q-a<δ等價於a<p<a+δ,a<q<a+δ。令p<q,即得到a<p<q<a+δ,由此得證瑕積分的柯西收斂準則。
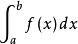 柯西極限存在準則
柯西極限存在準則(x=b是瑕點)同理可證。
項級數
定義
所謂函式列指的是,具有相同定義域的一列函式f(x),f(x),f(x),……所構成的集合{f(x)},可以簡寫成{f}。
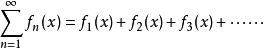 柯西極限存在準則
柯西極限存在準則而函式項級數,則是由這無窮多個函式相加所構成的級數
關於函式列和函式項級數收斂的定義,又有如下幾種:
(1)函式列(函式項級數)在某一點收斂
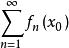 柯西極限存在準則
柯西極限存在準則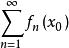 柯西極限存在準則
柯西極限存在準則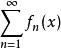 柯西極限存在準則
柯西極限存在準則設x為定義域上的某一點,那么f(x)是某個具體的常數,因此函式列{f(x)}(或函式項級數 )就轉化為一個數列(或數項級數)。如果當n趨於無窮大時,這個數列(或數項級數)的極限存在,則稱函式列{f(x)}(或函式項級數 )在x=x處收斂,而把x稱作函式列{f}(或函式項級數 )的收斂點。
並把所有收斂點構成的集合稱為收斂域。顯然,收斂域是定義域的一個子集。
(2)極限函式與和函式
對於收斂域內任意一個數x,函式列(或函式項級數)成為一收斂的數列(或數項級數),因而有確定的函式值y(或和s)。通過這種對應關係,在收斂域上就定義了一個函式列的極限函式(或函式項級數的和函式),寫作f(x)(或s(x)),並有:
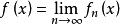 柯西極限存在準則
柯西極限存在準則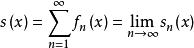 柯西極限存在準則
柯西極限存在準則(或 ,s(x)是函式項級數前n項的部分和)
註:顯然函式項級數前n項的部分和s(x)所構成的集合{s(x)}同樣是一個函式列,並且s(x)=f(x)+f(x)+……+f(x)。
利用ε-N語言,可以精確地定義極限函式:
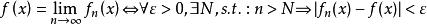 柯西極限存在準則
柯西極限存在準則(3)函式列(函式項級數)的一致收斂
根據(2)中極限函式的定義,我們可以知道函式列{f}具有極限函式的充要條件是:對任意ε>0,總存在正整數N,使得當n>N時,有|f(x)-f(x)|<ε。通常這個N不僅與ε有關,也與自變數x有關,就算ε不變,當x發生改變時,N也會隨之改變。但是,如果某一函式列能找到這樣一個正整數N,它只與ε有關,而對定義域(或其某個子集)上的任意一點x這個N都適用。即對任何x∈D(D是函式列的定義域或其某個子集),只要n>N時,就有|f(x)-f(x)|<ε。對於函式列的這種性質我們給它一個專門的名詞,這就是下面要介紹的一致收斂。
設D是函式列{f}的定義域(或其某個子集),f是D上有定義的函式。如果對任意ε>0,總存在某一正整數N,使得當n>N時,對一切x∈D,都有|f(x)-f(x)|<ε,則稱函式列{f}在D上 一致收斂於f。
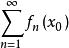 柯西極限存在準則
柯西極限存在準則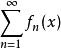 柯西極限存在準則
柯西極限存在準則又設{s(x)}是函式項級數 的部分和函式列,若{s(x)}在D上一致收斂於s(x),則稱函式項級數 在D上一致收斂於s(x)。
顯然,函式列在某個數集上即使處處都收斂(又叫逐點收斂),也不一定在該數集上一致收斂。但在數集上一致收斂時,必定在該數集上逐點收斂。逐點收斂和一致收斂的關係可以參考函式連續和一致連續的關係。
函式列和函式項級數的柯西收斂準則
(1)函式列的柯西收斂準則
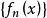 柯西極限存在準則
柯西極限存在準則函式列 在D上 一致收斂的充要條件是:對於任意給定的正數ε,總存在正整數N,使得當m,n>N時,對一切x∈D,有
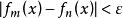 柯西極限存在準則
柯西極限存在準則(2)函式項級數的柯西收斂準則
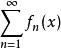 柯西極限存在準則
柯西極限存在準則函式項級數 在D上 一致收斂的充要條件是:對於任意給定的正數ε,總存在正整數N,使得當m>n>N時,對一切x∈D,有
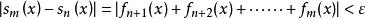 柯西極限存在準則
柯西極限存在準則證明
(1)函式列的柯西收斂準則
必要性
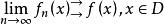 柯西極限存在準則
柯西極限存在準則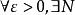 柯西極限存在準則
柯西極限存在準則設 ,則 ,當m,n>N時,對任意x∈D,有
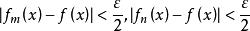 柯西極限存在準則
柯西極限存在準則那么,
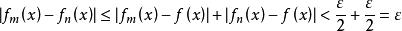 柯西極限存在準則
柯西極限存在準則充分性
由於對確定的x∈D,{f}為某一確定的數列,因此根據數列的柯西收斂準則,當x取遍D上的每一點時,函式列{f}總收斂,設其極限函式為f。
現只需要證明,{f}一致收斂於f。
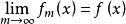 柯西極限存在準則
柯西極限存在準則事實上,由於已證得 ,根據極限的定義,對任意給定的正數ε,總存在正整數N,使得當m>N時,有
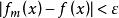 柯西極限存在準則
柯西極限存在準則於是,當n>N時,
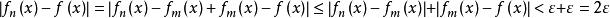 柯西極限存在準則
柯西極限存在準則這裡的ε和N都是柯西條件中的,即N只和ε有關,而對一切x∈D都適用。
因此根據一致收斂的定義,{f}一致收斂於f。
(2)函式項級數的柯西收斂準則
根據函式項級數一致收斂的定義,我們只需要證明部分和函式列{s(x)}在D上一致收斂於s(x)。顯然,{s(x)}一致收斂於s(x)的充要條件即是:對於任意給定的正數ε,總存在正整數N,使得當m>n>N時,對一切x∈D,有
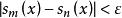 柯西極限存在準則
柯西極限存在準則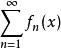 柯西極限存在準則
柯西極限存在準則那么,函式項級數 一致收斂的充要條件亦即是:對於任意給定的正數ε,總存在正整數N,使得當m>n>N時,對一切x∈D,有
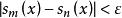 柯西極限存在準則
柯西極限存在準則
