極限定義
數列極限
數列極限定義：設為一無窮數列，如果存在常數，對於任意給定的正數（不論它多么小），總存在正整數，使得當時的一切，均有不等式成立，那么就稱常數是數列的極限，或稱數列收斂於。
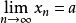極限理論記為或用邏輯符號可以表示為：
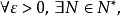極限理論當時，有
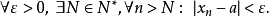極限理論或者：函式極限
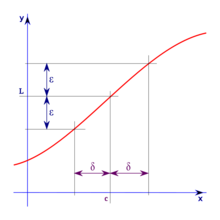
函式極限定義：設函式在點的某一去心鄰域內有定義，如果存在常數，對於任意給定的正數（無論它多么小），總存在正數，使得當滿足不等式時，對應的函式值滿足不等式，那么常數就叫做函式當時的極限，或稱函式收斂於.
極限理論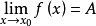
極限理論記為或用邏輯符號可以表示為：
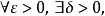極限理論當時，有歷史背景
牛頓微積分一誕生，就在力學、天文學中大現身手，能夠輕而易舉地解決許多本來認為束手無策的難題。後來，微積分又在更多的領域取得了豐碩的成果。人們公認微積分是17、18世紀數學所達到的最高成就，然而它的創始人牛頓和萊布尼茨對之所作的論證卻並不清楚、很不嚴謹。無論是牛頓的瞬和流數，還是萊布尼茨的dx和，都涉及到"無窮小量"，而在他們各自的論述中都沒有給出確定的、一貫的定義。在微積分的推導和運算過程中，常常是先用無窮小量作為分母進行除法，然後又把無窮小量當作零，以消除那些包含有它的項。那么"無窮小量"究竟是零還是非零呢？如果它是零，怎么能用它去作除數呢？如果它不是零，又怎么能把包含它的那些項消除掉呢？這種邏輯上的矛盾，牛頓和萊布尼茨都意識到了。牛頓曾用有限差值的最初比和最終比來說明流數的意義，但是當差值還未達到零時，其比值不是最終的，而當差值達到零時，它們的比就成為，怎樣理解這樣的最終比呢？實在令人困惑。牛頓承認他對自己的方法只作出"簡略的說明，而不是正確的論證。"萊布尼茨曾把無窮小量形容為一種"理想的量"，但正如一些數學家所說："與其說是一種說明，還不如說是一個謎。"
奇怪的是，微積分自身存在著明顯的邏輯混亂，然而在實際套用中則是卓有成效的得力工具。這樣，微積分就具有了"神秘性"。起初，"神秘性"集中表現在對於"無窮小量"這個概念的理解上，並因而受到了各種人的攻擊。數學家們不能容忍這一新方法的理論本身是如此的含糊不清乃至荒謬絕倫。法國數學家洛爾稱微積分為"巧妙的謬論的匯集"；著名思想家伏爾泰說微積分是"精確的計算和度量某種無從想像其存在的東西的藝術"。在一片疑難和責問聲中，以英國主教兼哲學家貝克萊的譴責最為強烈，他譏諷無窮小量是"逝去的量的鬼魂"，說微積分包含"大量的空虛、黑暗和混亂"，是"分明的詭辯"。
達朗貝爾馬克思曾對微積分作過一番歷史考察，他把這一時期稱為"神秘的微積分"時期，並有這樣的評論："於是，人們自己相信了新發現的算法的神秘性。這種算法肯定是通過不正確的數學途徑得出了正確的（而且在幾何套用上是驚人的）結果。人們就這樣把自己神秘化了，對這新發現的評價更高了，使一群舊式正統派數學家更加惱怒，並且激起了敵對的叫囂，這種叫囂甚至在數學界以外產生了反響，而為新事物開拓道路，這是必然的。"
微積分的邏輯缺陷和人們的猛烈攻擊，激厲數學家們為消除微積分的神秘性，亦即為微積分建立合理的理論基礎而努力。18世紀，在這方面作出貢獻的主要代表人物是達朗貝爾、歐拉和拉格朗日。可是"無窮小量"的本質尚未弄明白，無窮級數的"和"的問題又日漸突出了。在微積分里，一個典型的基本算法就是把無窮多項相加，叫做求無窮級數之和。在初等數學中，有限多項相加總有確定的和。而無窮多項相加，是加不完的，什麼是無窮級數的"和"是不清楚的。在很長一段時間裡，人們習慣地把有限多項相加的運算規則照搬到無窮級數中，雖然也解決過許多問題，但有時竟出現了像1/2=0這樣的荒謬結果。
柯西進入19世紀以後，隨著微積分套用的更加廣泛和深入，遇到的數量關係也更加複雜，很多問題，例如，對於熱傳導現象的研究，就已超出了早年力學那樣的直觀性。在這種情況下，要求有明確的概念、合乎邏輯的推理和運算法則，就顯得更加重要和迫切了。事實上，微積分作為變數數學，是運用"無窮"來描畫和研究運動和變化過程，獲得了成功的，卻長期沒有對有關"無窮"的概念給出正確的闡述，甚至導致邏輯上的混亂，微積分的神秘性正是由此而來，而這也正是微積分的理論基礎所要解決的問題。
數學家們經過一百多年的艱苦探索歷程，終於在前人所積累的大量成果（包括許多失敗的嘗試）的基礎上，建立起微積分的理論基礎。柯西(1789―1857）於1821年出版的《分析教程》中，開始有了極限概念的基本明確的敘述，並以極限概念為基礎，對"無窮小量"、無窮級數的"和"等概念給出了比較明確的定義。例如，從極限的觀點看，"無窮小量"就是極限為零的變數，在變化過程中，它可以是"非零"，但它的變化趨向是"零"，無限地接近於"零"。極限論正是從變化趨向上說明了"無窮小量"與"零"的內在聯繫，從而澄清了邏輯上的混亂，撕下了早期微積分的神秘面紗。後來，經過波爾察諾、魏爾斯特拉斯、戴德金、康托等人的卓越工作，又進一步把極限論建立在嚴格的實數理論基礎上，並且形成了描述極限過程的ε-δ語言。微積分理論基礎的嚴密化，使微積分躍進和擴展為現代數學的重要領域。
魏爾斯特拉斯微積分的發展歷史告訴我們，一門學科不能只停留在感性階段，如果不上升到理性，不具備堅實的理論基礎，不但其套用受到限制，學科本身也難以繼續發展。然而在上一世紀我國的多次運動中，在"數學是唯心主義的世襲領地"這種錯誤思想影響下，極限論和ε-δ語言屢遭批判，屢次被攆出課堂。"文革"之後，一位教師感慨地說："當我做學生的時候，也曾起勁地參加批判，但畢業以後，做了幾年教學工作，我體會到過去批判的東西其實是正確的、有重要意義的。可是當我向學生講述這些道理的時候，我自己卻又成為學生們的批判對象了。"
恩格斯早就指出："一個民族想要站在科學的最高峰，就一刻也不能沒有理論思維。"
