布爾代數
 布爾代數
布爾代數是一個集合 A,提供了兩個二元運算 <math>\land</math> (邏輯與)、<math>\lor</math> (邏輯或),一個一元運算 <math>\lnot</math> / ~ (邏輯非)和兩個元素 0(邏輯假)和 1(邏輯真),此外,對於集合 A 的所有元素 a、b 和 c,下列公理成立:
<math> a \lor (b \lor c) = (a \lor b) \lor c </math> <math> a \land (b \land c) = (a \land b) \land c </math> 結合律
<math> a \lor b = b \lor a </math> <math> a \land b = b \land a </math> 交換律
<math> a \lor (a \land b) = a </math> <math> a \land (a \lor b) = a </math> 吸收律
<math> a \lor (b \land c) = (a \lor b) \land (a \lor c) </math> <math> a \land (b \lor c) = (a \land b) \lor (a \land c) </math> 分配律
<math> a \lor \lnot a = 1 </math> <math> a \land \lnot a = 0 </math> 互補律
上面的前三對公理: 結合律、交換律和吸收律,意味著 (A, <math>\land</math>, <math>\lor</math>) 是一個格。所以布爾代數也可以定義為一個分配的有補格。
從這些公理,你可以展示出最小元素 0、最大元素 1 和任何元素 a 的補 ¬a 都是唯一確定的。對於 A 中的所有的 a 和 b,下列恆等式也成立:
<math> a \lor a = a</math> <math> a \land a = a </math> 冪等律
<math> a \lor 0 = a </math> <math> a \land 1 = a </math> 有界律
<math> a \lor 1 = 1 </math> <math> a \land 0 = 0 </math>
<math> \lnot 0 = 1 </math> <math> \lnot 1 = 0 </math> 0 和 1 是互補的
<math> \lnot (a \lor b) = \lnot a \land \lnot b</math> <math> \lnot (a \land b) = \lnot a \lor \lnot b</math> de Morgan 定律
<math> \lnot \lnot a = a </math> 對合律
例子
最簡單的布爾代數只有兩個元素0和1,並通過如下規則定義:
∧ 0 1
0 0 0
1 0 1
∨ 0 1
0 0 1
1 1 1
它套用於邏輯中,解釋 0 為假,1 為真,∧ 為與,∨ 為或,¬ 為非。 涉及變數和布爾運算的表達式代表了陳述形式,兩個這樣的表達式可以使用上面的公理證實為等價的,若且唯若對應的陳述形式是邏輯等價的。
兩元素的布爾代數也是在電子工程中用於電路設計;這裡的 0 和 1 代表數字電路中一個位的兩種不同狀態,典型的是高和低電壓。電路通過包含變數的表達式來描述,兩個這種表達式對這些變數的所有的值是等價的,若且唯若對應的電路有相同的輸入-輸出行為。此外,所有可能的輸入-輸出行為都可以使用合適的布爾表達式來建摸。
兩元素布爾代數在布爾代數的一般理論中也是重要的,因為涉及多個變數的等式是在所有布爾代數中普遍真實的,若且唯若它在兩個元素的布爾代數中是真實的(這總是可以通過平凡的蠻力算法證實)。比如證實下列定律(合意(Consensus)定理)在所有布爾代數中是普遍有效的:
(a ∨ b) ∧ (¬a ∨ c) ∧ (b ∨ c) ≡ (a ∨ b) ∧ (¬a ∨ c)
(a ∧ b) ∨ (¬a ∧ c) ∨ (b ∧ c) ≡ (a ∧ b) ∨ (¬a ∧ c)
任何給定集合S的冪集(子集的集合)形成有兩個運算∨:=∪(並)和∧:=(交)的布爾代數。最小的元素0是空集而最大元素1是集合S自身。
有限的或者 cofinite 的集合 S 的所有子集的集合是布爾代數。
對於任何自然數 n,n的所有正約數的集合形成一個分配格,如果我們對 a | b 寫 a ≤ b。這個格是布爾代數若且唯若 n 是無平方因子的。這個布爾代數的最小的元素0是自然數 1;這個布爾代數的最大元素 1 是自然數 n。
布爾代數的另一個例子來自拓撲空間: 如X是一個拓撲空間,它既是開放的又是閉合的,X 的所有子集的蒐集形成有兩個運算∨:= ∪(並)和∧ := ∩(交)的布爾代數。
如果R是一個任意的環,並且我們定義中心冪等元(central idempotent)的集合為
A ={ e ∈ R : e2 = e, ex = xe, ∀x ∈ R }
則集合A成為有兩個運算 e ∨ f := e + f + ef 和 e ∧ f := ef 的布爾代數。
正文
首先是G.布爾為了研究思維規律(邏輯學、數理邏輯)於1847年和1854年提出的。它作為一種特殊的格則是J.W.R.戴德金之後的事情。所謂一個布爾代數,是指一個有序的四元組〈B,∨,∧,* 〉,其中B是一個非空的集合,∨與∧ 是定義在B上的兩個二元運算,*是定義在B上的一個一元運算, 並且它們滿足以下條件:A1.α∨b=b∨α,α∧b=b∧α;A2.(α∨b)∨с=α∨(b∨с), (α∧b)∧с=α∧(b∧с); A3.(α∧b)∨b=b, (α∨b)∧b=b; A4.α∧(b∨с) = (α∧b)∨(α∧с),α∨(b∧с)=(α∨b)∧(α∨с);A5.(α∧α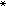 )∨b=b,(α∨α
)∨b=b,(α∨α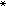 )∧b=b,對於任意的α、b、с∈B均成立。或者,布爾代數定義為具有最大元和最小元的有餘(有補)的分配格。
)∧b=b,對於任意的α、b、с∈B均成立。或者,布爾代數定義為具有最大元和最小元的有餘(有補)的分配格。
設B2={0,1}是由兩個元素0與1所組成的集合。它的兩個二元運算和一個一元運算定義如下:0∨0=0,0∨1=1∨0=1∨1=1;0∧0=0∧1=1∧0=0,1∧1=1;0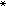 =1,1
=1,1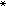 =0。可以驗證,B2是一個布爾代數。
=0。可以驗證,B2是一個布爾代數。
設B={1,2,3,5,6,10,15,30}是30的正因子的集合。規定∨是取它們的最低公倍數,∧是取它們的最大公因數:*是:1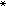 =30,2
=30,2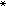 =15,3
=15,3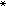 =10,5
=10,5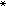 =6,6
=6,6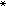 =5, 10
=5, 10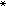 =3,15
=3,15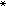 =2,30
=2,30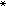 =1,容易驗證B對於所定義的運算成為一布爾代數。
=1,容易驗證B對於所定義的運算成為一布爾代數。
如果一個環R=〈R,+,·〉具有單位元1,並且對任意的α∈R,有α2 =α,那么R稱為布爾環。令R是布爾環,若定義α∨b=α+b+α·b,α∧b=α·b,α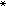 =1+α,則R在所定義的運算下成為一個布爾代數。
=1+α,則R在所定義的運算下成為一個布爾代數。
設R是由所有的實數組成的集合。由單元集和區間的有限並所組成的集合B,在集合的並(∪)、交(∩)、余(C)運算之下是一個布爾代數。所謂單元集,是指僅由一個實數所組成的集合。區間可以是有界的或無界的,閉的或開的或半開(閉)的。
令Χ是一個固定的集合。Χ的所有子集組成的集合稱為Χ的冪集,記為P(Χ)={S│S⊆Χ}。設B是P(Χ)的子集,並且{═,Χ}⊆B⊆P(Χ)。如果B在集合論的並(∪)、交(∩)、余(C)有限次運算下是封閉的,那么這樣的B在把有限次並、交、余作為∨、∧、*運算時,是一個布爾代數。這種布爾代數,常常稱為集域(集場)。特殊地,取B=B2={═,Χ},B=P(Χ),B={S∈P(Χ)│S為有限集或有限集的余集},……,均為集域。當Χ={α1,α2,…,αn}是有限集時,則P(Χ)={S│S⊆Χ}={{αi1,αi2,…,αik}│i1,i2,…,ik是1,2,…,n中取k個的組合,0≤k≤n}=2X =2n 也是一個集域。它是由有限個元素所組成的布爾代數(有限布爾代數)。
令〈Χ,τ〉是一個拓撲空間,τ是 X上的一個拓撲,B={S⊆Χ│S 既是開集,同時又是閉集}。在集合論的並、交、余運算下B是一個布爾代數,並稱之為閉開代數。若取B={S⊆Χ│S的邊界是無處稠密的},則此時B也是一個布爾代數。
令〈Χ,τ〉是一個拓撲空間,Χ的子集S是正規的閉集,若且唯若S的內部的閉包等於S,即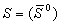 。若B={S⊆Χ│S是正規的閉集},二元運算∨是指集合的並運算,二元運算∧是指經集合的交運算後再取其內部的閉包,即
。若B={S⊆Χ│S是正規的閉集},二元運算∨是指集合的並運算,二元運算∧是指經集合的交運算後再取其內部的閉包,即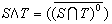 ,S、T∈B。一元運算*是指經集合的余運算後再取閉包,即
,S、T∈B。一元運算*是指經集合的余運算後再取閉包,即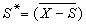 ,則B是一個布爾代數,也稱為拓撲空間 〈Χ, τ〉的正規閉集代數。類似地,當取B={S⊆Χ│S是正規的開集}。所謂正規的開集S,是指
,則B是一個布爾代數,也稱為拓撲空間 〈Χ, τ〉的正規閉集代數。類似地,當取B={S⊆Χ│S是正規的開集}。所謂正規的開集S,是指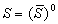 。再定義運算:
。再定義運算: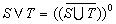 ,S∧T=S∩T;
,S∧T=S∩T;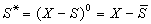 ,則此時 B也是一個布爾代數,也稱為正規開集代數。
,則此時 B也是一個布爾代數,也稱為正規開集代數。
在機率論中,設B={S│S是隨機事件},即所有隨機事件的全體。不可能事件及必然事件均視作隨機事件。這樣的B在邏輯聯結詞"或"(可得兼的"或")、“與”、“否定”運算之下是一個布爾代數。
在數理邏輯中,基於二值邏輯的一個形式理論的所有公式,在邏輯聯結詞“析取”、“合取”、“否定”運算下,是一個布爾代數,也稱之為林登鮑姆-塔爾斯基代數。
布爾代數到了20世紀30~40年代才又有了新的進展,大約在1935年,M.H.斯通首先指出布爾代數與環之間有明確的聯繫,他還得到了現在所謂的斯通表示定理:任意一個布爾代數一定同構於某個集上的一個集域;任意一個布爾代數也一定同構於某個拓撲空間的閉開代數等,這使布爾代數在理論上有了一定的發展。布爾代數在代數學(代數結構)、邏輯演算、集合論、拓撲空間理論、測度論、機率論、泛函分析等數學分支中均有套用;1967年後,在數理邏輯的分支之一的公理化集合論以及模型論的理論研究中也起著一定的作用。
近幾十年來,布爾代數在自動化技術、電子計算機的邏輯設計等等工程技術領域中有重要的套用。
例如,在邏輯設計中,要考慮取值於B2中的元素的布爾變元 x1,x2,…,xn,以及函式值也在B2內的n個布爾變元的布爾函式ƒ(x1,x2,…,xn)。令x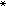 =1-x=x-1 ,x∨y=max{x, y},x∧y=min{x, y},於是任一布爾函式可表示成如下的形式:
=1-x=x-1 ,x∨y=max{x, y},x∧y=min{x, y},於是任一布爾函式可表示成如下的形式: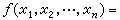
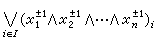 或
或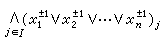 ,
,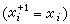 。這種形式稱為ƒ的(完全的)析取範式(或完全的合取範式)。根據設計要求可先列出真值表(ƒ的列表表示),由真值表寫出ƒ的析取範式(或合取範式)。化簡布爾函式的表達形式在實際套用中是特別重要的,因為根據最簡表達形式進行設計,不僅在功能(實際效果)上是等效的,而且更有意義的是這種設計簡單、經濟、可靠,因而壽命也長。化簡的方法,大體上從20世紀50年代開始有所謂卡諾圖的方法,奎因-麥克魯斯基方法等等。
。這種形式稱為ƒ的(完全的)析取範式(或完全的合取範式)。根據設計要求可先列出真值表(ƒ的列表表示),由真值表寫出ƒ的析取範式(或合取範式)。化簡布爾函式的表達形式在實際套用中是特別重要的,因為根據最簡表達形式進行設計,不僅在功能(實際效果)上是等效的,而且更有意義的是這種設計簡單、經濟、可靠,因而壽命也長。化簡的方法,大體上從20世紀50年代開始有所謂卡諾圖的方法,奎因-麥克魯斯基方法等等。
基本規則
代入法則它可描述為邏輯代數式中的任何變數A,都可用另一個函式Z代替,等式仍然成立。
對偶法則
它可描述為對任何一個邏輯表達式F,如果將其中的“+”換成“*”,“*”換成“+”“1”換成“0”,“0”換成“1”,仍保持原來的邏輯優先權,則可得到原函式F的對偶式G,而且F與G互為對偶式。我們可以看出基本公式是成對出現的,二都互為對偶式。
反演法則
有原函式求反函式就稱為反演(利用摩根定律),我們可以把反演法則這樣描述:將原函式F中的“*”換成“+”,“+”換成“*”,“0”換成“1”,“1”換成“0”;原變數換成反變數,反變數換成原變數,長非號即兩個或兩個以上變數的非號不變,就得到原函式的反函式。
布爾代數定律
互補律:
第一互補律: 若A=0,則~A=1,若A=1,則~A=0 註:~A =NOT A
第二互補律: A*~A=0
第三互補律: A+~A=1
雙重互補律: /<~A>=//A=A
交換律:
AND交換律: A*B=B*A
OR交換律: A+B=B+A
結合律:
AND結合律: A<B*C>=C*<A*B>
OR結合律: A+<B+C>=C+<A+B>
分配率:
第一分配率: A*<B+C>=<A*B>+<A*C>
第二分配率: A+<B*C>=*
重言律:
第一重言律: A*A=A 若A=1,則A*A=1;若A=0,則A*A=0。因此表達式簡化為A
第二重言律: A+A=A 若A=1,則1+1=1;若A=0,則0+0=0。因此表達式簡化為A
帶常數的重言律: A+1=1 A*1=A A*0=0 A+0=A
吸收率:
第一吸收率: A*=A
第二吸收率: A+=A

