奇函式

如果對於函式f（x）的定義域內任意一個x，都有f（-x）= - f（x），那么函式f（x）就叫做奇函式（odd function）。奇函式的定義域必須關於原點（0，0）對稱，否則不能成為奇函式。設f(x)在I上可導，若f(x)在I上為奇函式，則f'(x)在I上為偶函式。若且唯若f（x）=0（定義域關於原點對稱）時，f（x）既是奇函式又是偶函式。

基本信息

• 中文名：奇函式
• 其他外文名：odd function

• 形式：f（-x）= - f（x）
• 學科：數學

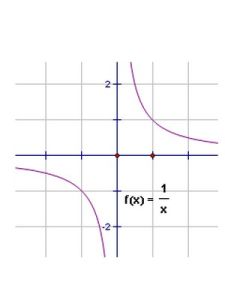
函式定義

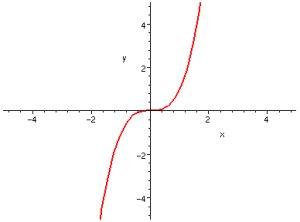奇函式

2、奇函式圖象關於原點（0，0）中心對稱。
3、奇函式的定義域必須關於原點（0，0）對稱，否則不能成為奇函式。
4、若F(X)為奇函式，定義域中含有0，則F(0)=0.1、在奇函式f（x）中，f（x）和f（-x）的符號相反且絕對值相等，即f(-x)=-f(x)，反之，滿足f(-x)=-f(x)的函式y=f（x）一定是奇函式。例如:f(x)=x^(2n-1),n∈Z;(f(x)等於x的2n-1次方,n屬於整數)
2、奇函式圖象關於原點（0，0）中心對稱。
3、奇函式的定義域必須關於原點（0，0）對稱，否則不能成為奇函式。
4、若F(X)為奇函式，定義域中含有0，則F(0)=0
相關函式：偶函式，非奇非偶函式
5、設f(x)在I上可導，若f(x)在I上為奇函式，則f'(x)在I上為偶函式。
即f(x)=-f(-x)對其求導f'(x)=[-f(-x)]'(-x)'=-f'(-x)(-1)=f'(-x)偶函式與奇函式滿足下列基本性質

運算法則

(1) 兩個偶函式相加所得的和為偶函式。(2) 兩個奇函式相加所得的和為奇函式。(3) 一個偶函式與一個奇函式相加所得的和為非奇非偶函式。(4) 兩個偶函式相乘所得的積為偶函式。(5) 兩個奇函式相乘所得的積為偶函式。(6) 一個偶函式與一個奇函式相乘所得的積為奇函式。(7) 若f(x)為奇函式，且f(x)在x=0時有定義，那么一定有f(0)=0。(8) 定義在R上的奇函式f（x）必定滿足f(0)=0。(9) 若且唯若f（x）=0（定義域關於原點對稱）時，f（x）既是奇函式又是偶函式。(10) 奇函式在對稱區間上的積分為零。

函式圖像

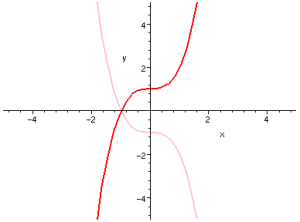奇偶函式

(1) 奇函式的圖象關於原點中心對稱。(2) 偶函式的圖象關於Y軸對稱。(3) 奇、偶函式的定義域一定關於原點對稱。(4) 奇函式的偶次項係數等於0，偶函式的奇次項係數等於0。(5) Y=0即是X軸，既是奇函式也是偶函式。

函式例子

奇函式：F（X）=-F(-X)，當在x=0處有定義時，有F（0）=0。常見的奇函式有F（X）=sinX。偶函式圖象關於Y軸對稱，F（x）=F（-X），如F（X）=cosX。對於函式y=ax^2+bx+c(a,b,c∈R)，當a=0,b=0,c=0時，f(x)既是奇函式又是偶函式，當b∈R,a=0,c=0時，f(x)是奇函式；當a∈實數R,b=0,c∈實數R時，f(x)是偶函式。