勒讓德多項式

勒讓德多項式是描述矩形表面和口徑的另外一組多項式集合，它的優點是具有正交性。由於存在正交性條件，高階項係數趨於零，並且增加和刪除一個項對其他項沒有影響。不過，這個多項式集合通常不在光學設計軟體中使用。

定義

定義一

勒讓德多項式的數學描述如下 ：

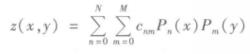勒讓德多項式

式中，

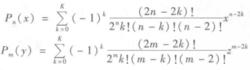勒讓德多項式

下圖為幾個低階的勒讓德多項式 ：

勒讓德多項式

勒讓德多項式

定義二

在區間[一1，1]帶權函式ρ(x)=1的正交多項式為

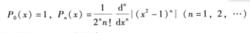勒讓德多項式

它稱為勒讓德(Legendre)多項式。

由於（x²-1）ⁿ是2n次多項式，求n階導數後．得到

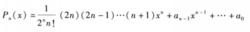勒讓德多項式

於是，得到首項(最高次項)xⁿ的係數

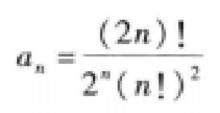勒讓德多項式

顯然．首項係數為1的勒讓德多項式為

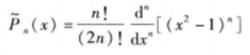勒讓德多項式

性質

正交性

1.

正交性

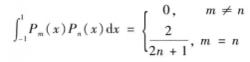勒讓德多項式

2.奇偶性

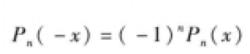勒讓德多項式

事實上，(x²—1)ⁿ是偶函式，經過偶數次求導仍為偶函式，經過奇數次求導仍為奇函式，故由式

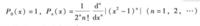勒讓德多項式

知，n為偶數時Pn(x)為偶函式，n為奇數時Pn(x)為奇函式，奇偶性成立。

3.遞推關係

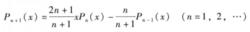勒讓德多項式

由P0(x)=1，P1(x)=x，利用上式就可推出

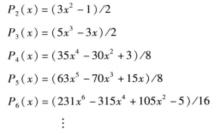勒讓德多項式

下圖給出了P0(x)，P1(x)，P2(x)，P3(x)的圖形。

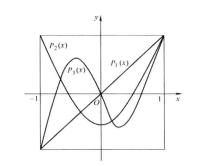勒讓德多項式

4. Pn(x)在區間(一1，1)內有n個不同的實零點 。