性質
曲面Σ上過點 M的所有曲線在點M處的切線都位於曲面Σ在切點 M處的 切平面。
證明
球面的切平面
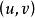切平面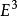
切平面
切平面
切平面
切平面設正則參數曲 S的方程為 ， 是曲面 S上點的曲紋坐標，因此曲面 S上的任意曲線L可以用參數方程 給出，將其視為 中的曲線，則其方程為 。
切平面顯然，根據定義， 都是曲面 S的切向量，假定 P是曲線上對應t=0的點，因此曲面 S在點 P的切向量是
切平面
切平面
切平面
切平面
切平面
切平面 切平面這表明曲面 S在 P點的切向量為，是，的線性組合，其分量恰好是，。反過來，的任意一個線性組合必定是曲面的切向量。
切平面
切平面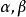
切平面
切平面
切平面
切平面實際上，對於任意實數，只要命曲線L為，，其中，，則曲線 L在點 P的切向量是.
切平面 切平面
切平面
切平面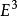 切平面 切平面由於,故是線性無關向量，因此曲面在點 P的切向量構成一個二維向量空間，這個空間稱為曲面 S在點 P的切空間，記做，顯然，構成了空間的一個基底。在空間中經過點 P、並且由空間 S在點 P張成的平面就是曲面 S在點 P的切平面，顯然，曲面在點 P的切平面是與曲面的參數表示無關的概念。
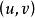切平面 切平面
切平面曲面在點的切平面的參數方程是.
舉例
平面的切平面為此平面自身。
錐面的所有切平面都經過一個定點
