二次曲面束

pencil of conicoids 在射影空間內，兩個二次曲面□和□可交成一條空間四次曲線。特殊時，當兩個二次曲面是直紋曲面，且有一條公共母線，則這條四次曲線將為一直線（即公共母線）和一條三次曲線。與二次曲束的定義相似，通過□□=0和□□=0交線的二次曲面的全體，叫做二次曲面束。

二次曲面束

正文

在射影空間內，兩個二次曲面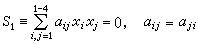

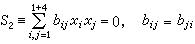
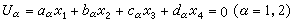和

可交成一條空間四次曲線。特殊時，當兩個二次曲面均是直紋曲面，且有一條公共母線，則這條四次曲線將表為一直線（即公共母線）和一條三次曲線。與二次曲線束的定義相似，通過S1=0和S2=0交線的二次曲面的全體，叫做二次曲面束。它的方程可寫作：S1-λS2=0，其中λ是參數，由於S1=0和S2=0相交成四次曲線，故束中各曲面必通過這四次曲線。若已知一個二次曲面S=0和兩個平面,且相交產生兩個平截線,則過兩個平截線的二次曲面束可寫作:S-λU1U2=0，這裡λ是參數，平面偶U1U2＝0可作為一個退化二次曲面。又若已知八個定點Pi(i=1,2,…,8)，可另取不同於Pi的二定點A及B,則由二次曲面的方程可知,通過九個點的二次曲面是惟一確定的，於是 Pi(i=1,2,…,8)和A或B分別決定兩個二次曲面S1=0和S2=0，又因二次曲面束通過S1=0,S2=0的所有公共點,故也必通過八個定點Pi，而且S1=0,S2=0,的交線為四次曲線,故過八個定點的二次曲面束，必過一條四次曲線。
和二次曲線束的性質相類似，對於二次曲面束，有以下的性質：①一個定點關於二次曲面束所有曲面的極平面必為一平面束；②一個定平面關於二次曲面束所有曲面的極點，為一條三次曲線；③一定直線關於二次曲面束所有曲面的極線，為一環形（或管形）曲面。
參考書目
　方德植、陳奕培編：《射影幾何》，高等教育出版社，北京，1983。
　W.C.Graustein,Higher Geometry,Macmillan, New York, 1948.

配圖

相關連線