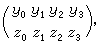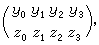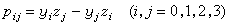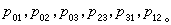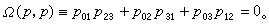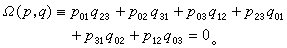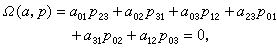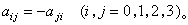直線幾何

直線幾何是以直線為基本元素的幾何學。人們習慣於以點為幾何基本元素,而把其他幾何圖形作為點的集合。但是,也可以把其他一些幾何對象作為基本元素。

直線幾何

正文

以直線為基本元素的幾何學。人們習慣於以點為幾何基本元素,而把其他幾何圖形作為點的集合。但是,也可以把其他一些幾何對象作為基本元素。例如以直線為元素就有直線幾何學，以平面上的圓或三維空間的球面作為基本元素，就有圓素或球素幾何學,等等。這樣,以點為基本元素的幾何就可以叫做點幾何學。
射影平面p2上的直線幾何只是點幾何的對偶。三維射影空間p3的直線構成一個四參數族，p3的直線幾何值得特別注意。
直線坐標　設在三維射影空間p3里，建立了齊次坐標系。p3里的一條直線p可以用它上面兩點(y),(z)來決定。取這兩點的坐標所構成的矩陣

令

表示矩陣的二階行列式,則pij＝-pij。因此,可以省掉pij中的一半，剩下六個：

容易證明：如果在p上取任意其他兩點來代替(y)，(z)，所得到的pij和原來的成比例；還可以證明,上述六個pij滿足一個二次方程

倒轉來,已給不都等於零而滿足Ω(p,p)=0的六個pij，必有惟一的一條直線，它上面兩點的坐標所構成的二階行列式和所給pij成比例。因此,不都等於零而滿足Ω(p，p)＝0的六個pij 總可以看做p3里一條直線p 的齊次坐標(p)=(pij)，叫做普呂克坐標。
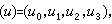
p3里一條直線也可以看做兩個平面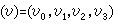的交線。令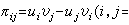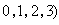，不難證明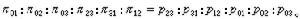
相交直線　兩條直線p，q相交的充要條件是它們的坐標(p)，(q)滿足雙線性方程

線束、線把與線場　兩條直線p，q的坐標(p)，(q)的線性組合(λp＋μq)一般不是一條直線的坐標。三條直線的坐標的線性組合也是如此。但是，①若p，q為相交直線，則當(λ,μ)≠(0,0)時, 線性組合(λp＋μq)代表直線，而且一切這樣的直線構成p，q所確定的線束；②若p,q,r為共點而不共面的直線, 則(λ,μ,v)≠(0,0,0)時，線性組合(λp＋μq＋vr)也代表直線,而一切這樣的直線構成p，q，r所確定的線把；③若p，q,r為共面而不共點的直線，則它們的一切線性組合(其中係數不都是零)構成它們所確定的線場。
線叢、線匯與線列　含直線坐標的一個齊次方程代表一個線叢；兩個獨立聯立方程代表一個線匯；三個獨立聯立方程代表一個線列。一般地，它們依次含有∞3，∞2，∞1條直線。若這些方程是線性的，就有以下事實。 ①一個線性方程

式中αij是常數，代表一個線性線叢。若αij是一條固定直線α的坐標，則Ω(α,p)是一個“特殊線性線叢”，它是一切同α相交的直線所構成。若αij不是一條直線的坐標，則經過空間每一點或在每一個平面上，線叢的直線構成一個線束，這樣，在p3里，線叢里線束的頂點和它所在的平面之間，就建立了一宗一一對應關係，叫做零配極系。若(xj)和(uj)依次表示點坐標和平面坐標，則零配極系中的點面對應可以寫成

式中(αij)是反稱方陣，

② 兩個線性無關的線性方程聯立起來代表一個線性線匯，最一般的線性線匯是由一切同兩條相錯的固定直線都相交的直線所構成。
③ 三個線性無關的線性方程一般地代表一個二次線列，即一個直紋二次曲面的一族母線。
用點表示直線　如果把pij看作五維射影空間p3的齊次點坐標,則Ω(p,p)=0代表p3里的一個滿秩二次超曲面V,它的點和p3里的直線一一對應。經過p3里的一個坐標變換,這個V 的方程可以化為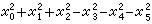＝0。p3里兩條相交的直線對應於p3里 V上兩個對於V 共軛的點。
每一個關於p3里直線的命題，對應於一個關於p3里V的命題。①p3里的線束對應於V上的直線，V上有∞3條直線。②p3里的線把或線場都對應於V上的平面。V上的平面構成兩個三參數族，一族代表p里的線把,另一族代表線場；同一族的兩個平面總有惟一的一個公共點；不同族的兩個平面一般不相交，如果相交，就交於一條直線。③p3里一個線性線叢對應於p3里一個超平面和V 的交集，即一個三維二次曲面；p3里的一個特殊線性線叢對應於p3里V的一個超切面和V的交集，即一個三維二次錐面。④p3里一個線性線匯對應於p3里一個三維平面和V 的交集,即一個二維二次曲面V；一般地，它上面的點都和V上兩個點共軛。⑤p3里的一個二次線列一般地對應於p3里V上一條二次曲線。
格拉斯曼坐標和格拉斯曼流形　作為以上事實的推廣，可以考慮n維射影空間Pn里的k維平面(1≤k≤n-1)。在k維平面上取k+1個獨立點,以它們的齊次坐標為行,就得到一個(k+1,n+1)矩陣，這個矩陣的k+1階行列式可以作為Pn里k維平面的齊次坐標（格拉斯曼坐標）,它們滿足若干個二次式。把這些坐標看作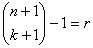維射影空間Pr的點的齊次坐標，就可以得到Pn里的k維平面和Pr里一個(n-k)(k+1)維流形 (格拉斯曼流形)上的點的一宗一一對應關係。
參考書目
　D.M.Y.Sommerville,Analytical Geometry of Three Dimensions,Cambridge Univ.Press,London,1934Oakley Sunglasses
http://www.oakleysunglassesshops.com
http://www.oakleysunglassesshops.com/oakley-lifestyle-sunglasses.html.

配圖

相關連線