公式
 已復原的正方形SQ1
已復原的正方形SQ1Square-1有人也稱之為“扇形魔方”,是由於SQ1在某種打亂的狀態是極像扇子狀的原因。SQ1是由Karel Hrsel和Vojtech Kopsky在1992年共同發明的。正方形SQ1屬於兩極類魔方中最常見的一種。我們平時說的SQ1魔方,通常都是指正方形的SQ1,當然,SQ1還有許多其他派生形狀的,如SSQ1(Super Square One)。SQ1的復原,它面臨著雙重困難:1,初始形狀的復原。2,色向塊的復原。它的難度主要在於上下兩個極面的方塊被切割成了可以轉動30度的小塊,從而可以產生不同於原始方方正正模樣的狀態。一般來說,如果能在SQ1的兩種經典型之間任意轉換,就證明已經基本掌握了SQ1的復原。
Square 1分為三層。頂層和底層都有風箏塊和三角塊,它們也被稱為角塊和邊塊。整個魔方總共有8個角塊和8個邊塊和2箇中層塊。相對於中層來講,角塊為60度,邊塊寬度為30度。
公式符號
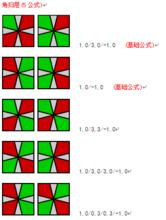 sq1魔方
sq1魔方/ 表示右半個魔方180°;6 6 表示前片(上片)順時針6×30°,後片(下片 )順時針6×30°。
如果是 3 -1,則表示前片順時針3×30°,後片逆時針1×30°,以次類推。注意:順、逆都是指面對被轉面看入魔方時的轉向!
0表示不轉。除了上下層可以轉動外,左右只有一種轉法,一般默認,一個公式的初態是約定中層的轉縫在前面是出現在偏左的位置,除非教程另有交代。
SQ1還原法
第一步
| 重要技巧 : 把所有的小棱集中起來 , 讓底層只有六個角塊形成一個六角星 , 於是便可以輕鬆得到以下左數起第一對形狀了 | ||
| 0 | /(-2,-4)/(-1,-2)/(-3,-3)/ | |
| 1 | /(2,-2)/(-3,-4)/(4,-3)/(-5,-4)/(6,-3)/ | |
| 2 | /(-4,-2)/(-1,4)/(-3,0)/ | |
| 3 | /(-4,0)/(5,4)/(2,-3)/(-5,-4)/(6,-3)/ | |
| 4 | /(2,2)/(0,-1)/(3,3)/ |
第二步
| (1,0) / (3,0) / (-1,0) |
| (1,0) / (-1,0) | (1,0) / (0,3) / (0,3) / (-1,0) |
| (1,0) / (3,0) / (3,0) / (-1,0) | (1,0) / (3,3) / (-1,0) |
第三步
這一步是把小刀變成一面,就象三階的OLL
| (0,-1) / (-3,0) / (4,1) / (-4,-1) / (3,0) / (0,-1) |
| (0,-1) / (3,0) / (-3,0) / (1,-2) / (0,3) / (-1,0) | (0,-1) / (1,1) / (-1,0) |
| (1,0) / (-3,0) / (-1,-1) / (4,1) / (-1,0) | (0,-1) / (3,0) / (0,-3) / (1,-2) / (3,0) / (-1,0) |
| (0,-1) / (1,4) / (-1,-4) / (-3,0) / (4,1) / (-1,0) | (0,-1) / (1,1) / (3,3) / (-1,-1) / (0,1) |
第四步
把各角塊調到正確的位置
| / (3,-3) / (3,0) / (-3,0) / (0,3) / (-3,0) / | / (3,3) / (3,0) / (3,3) / (3,0) / (3,3) / | / (3,-3) / (0,3) / (-3,0) / (3,0) / (-3,0) / | / (3,3) / (0,3) / (3,3) / (0,3) / (3,3) / |
| / (-3,0) / (3,3) / (0,-3) / | / (0,3) / (0,-3) / (0,3) / (0,-3) / | / (3,0) / (-3,0) / (3,0) / (-3,0) / | / (3,-3) / (3,-3) / |
第五步
開始細調各小刀的位置直到位置完全正確,即邊成為一片色
| 頂層 | 底層 | |
| (UR UF) / (-3,0) / (0,3) / (0,-3) / (0,3) / (2,0) / (0,2) / (-2,0) / (4,0) / (0,-2) / (0,2) / (-1,4) / (0,-3) / (0,3) [13|27] | ||
| (UR UL) / (3,3) / (-1,0) / (2,-4) / (4,-2) / (0,-2) / (-4,2) / (1,-5) / (3,0) / (3,3) / (3,0) [10|26] |
| 頂層 | 底層 | |
| (UR UB) (UL UF) / (3,3) / (0,3) / (1,1) / (-1,-4) / (-3,-3) / [6|15] | ||
| (UR UL) (UF UB) / (3,-3) / (3,-3) / (0,1) / (-3,3) / (-3,3) / (-1,0) [6|16] | ||
| (UR UL UB) / (3,0) / (1,0) / (0,-3) / (-1,0) / (-3,0) / (1,0) / (0,3) / (-1,0) [8|16] | ||
| (UR UB UL) (1,0) / (0,-3) / (-1,0) / (3,0) / (1,0) / (0,3) / (-1,0) / (-3,0) / [8|16] |
| 頂層 | 底層 | |
| (UR UF UL UB) (1,0) / (2,2) / (0,-2) / (3,3) / (1,0) / (4,4) / (0,-2) / (2,2) / (0,-1) / (3,3) / [10|25] | ||
| (UR UB UL UF) / (-3,-3) / (0,1) / (-2,-2) / (0,2) / (-4,-4) / (-1,0) / (-3,-3) / (0,2) / (-2,-2) / (-1,0) [10|25] | ||
| (UR UB UF UL) (0,-1) / (1,-2) / (-4,0) / (0,3) / (1,0) / (3,-2) / (-4,0) / (-4,0) / (-2,2) / (-1,0) / (0,-3) / (-3,0) [11|26] |
| 頂層 | 底層 | |
| (UR UF) (DL DF) (1,0) / (0,3) / (-1,-1) / (1,-2) / (-1,0) [4|11] | ||
| (UF UB) (DR DB) (1,0) / (0,-1) / (0,-3) / (5,0) / (-5,0) / (0,3) / (0,1) / (5,0) [7|15] | ||
| (UF UB) (DF DB) (1,0) / (5,-1) / (-5,1) / (5,0) [3|9] |
| 頂層 | 底層 | |
| (UR UF) (UL UB) (DR DF) / (3,0) / (3,3) / (0,-3) / (4,-3) / (4,-2) / (2,-4) / (0,-4) / (3,0) / (-3,-3) / (-3,0) [10|25] | ||
| (UL UR) (UF UB) (DR DB) / (3,3) / (1,4) / (0,-4) / (4,-2) / (2,-4) / (0,-1) / (0,3) / (-3,-3) / (-3,0) / (0,-3) [10|25] | ||
| (UR UL UB) (DR DB) / (3,3) / (1,0) / (-2,0) / (-4,0) / (0,-4) / (0,-4) / (0,-2) / (0,5) / (3,3) / (0,-3) [10|22] | ||
| (UR UB UL) (DB DL) / (-3,-3) / (0,-5) / (0,2) / (0,4) / (0,4) / (4,0) / (2,0) / (-1,0) / (-3,-3) / (0,3) [10|22] | ||
| (UR UF) (UL UB) (DR DL) / (3,3) / (1,0) / (-2,4) / (2,-4) / (0,4) / (2,2) / (-3,0) / (-3,-3) / (-3,0) [9|23] | ||
| (UL UR) (UF UB) (DR DL) / (3,3) / (1,0) / (-2,4) / (2,-4) / (2,0) / (3,3) / (-3,0) / (3,3) / (3,0) [9|23] | ||
| (UR UL UB) (DF DB) / (3,0) / (-3,0) / (3,0) / (0,3) / (1,0) / (0,2) / (4,0) / (0,-4) / (2,0) / (0,5) / (3,3) / (0,-3) [12|25] | ||
| (UR UB UL) (DR DL) / (-3,-3) / (0,-5) / (-2,0) / (0,4) / (-4,0) / (0,-2) / (-1,0) / (0,-3) / (-3,0) / (3,0) / (-3,0) / (0,3) [12|25] |
| 頂層 | 底層 | |
| (UR UF UL UB) (DR DB) / (-3,0) / (-2,0) / (5,-1) / (-5,0) / (3,0) / (-3,0) / (0,1) / (-3,0) / (-3,0) / (-1,0) [10|21] | ||
| (UR UB UL UF) (DR DB) (1,0) / (3,0) / (3,0) / (0,-1) / (3,0) / (-3,0) / (5,0) / (-5,1) / (2,0) / (3,0) / [10|21] | ||
| (UR UL UB UF) (DL DB) (1,0) / (0,3) / (5,5) / (3,0) / (-3,0) / (1,1) / (-3,0) / (-1,6) [7|19] | ||
| (UR UF UL UB) (DF DB) (0,-1) / (1,1) / (-3,0) / (-1,-1) / (-3,0) / (1,1) / (5,0) [6|16] | ||
| (UR UB UL UF) (DF DB) (0,-1) / (1,1) / (3,0) / (-1,-1) / (3,0) / (1,1) / (5,0) [6|16] | ||
| (UR UL UB UF) (DR DL) (1,0) / (0,3) / (-1,0) / (0,3) / (1,0) / (2,2) / (0,1) / (0,3) / (1,0) / (-3,0) / (-1,0) [10|22] |
| 頂層 | 底層 | |
| (UR UF) (UL UB) (DL DF) (DR DB) (1,0) / (3,0) / (5,5) / (3,-3) / (1,1) / (-3,0) / (5,6) [6|17] | ||
| (UL UR) (UF UB) (DR DF) (DL DB) / (3,3) / (0,-3) / (1,-5) / (4,-2) / (-2,1) / (3,3) / [7|18] | ||
| (UR UF UB) (DR DF) (DL DB) (0,-1) / (0,-3) / (1,1) / (5,-3) / (3,0) / (-5,0) / (0,5) / (0,-3) / (-1,0) / (0,-5) [9|21] | ||
| (UR UB UF) (DR DF) (DL DB) (0,-1) / (1,0) / (0,3) / (0,-5) / (5,0) / (-3,0) / (-5,3) / (-1,-1) / (0,3) / (0,-5) [10|21] | ||
| (UL UR) (UF UB) (DL DR) (DF DB) (1,0) / (5,-1) / (3,3) / (1,1) / (3,-3) / (5,0) [5|15] | ||
| (UL UB UF) (DL DR) (DF DB) (1,0) / (-1,5) / (3,1) / (-3,0) / (0,5) / (0,-5) / (3,0) / (-5,0) / (0,-3) / (5,0) [9|21] | ||
| (UR UB UF) (DL DR) (DF DB) (1,0) / (0,3) / (5,0) / (-3,0) / (0,5) / (0,-5) / (3,0) / (-3,-1) / (1,-5) / (5,0) [10|21] | ||
| (UR UB UF) (DL DF DB) (1,0) / (5,-1) / (-5,1) / (-3,0) / (0,3) / (-1,-1) / (1,-2) / (-4,0) [7|19] | ||
| (UR UF UB) (DR DB DF) (1,0) / (-1,5) / (0,-3) / (-5,-5) / (-3,0) / (5,0) [5|13] | ||
| (UL UF UB) (DR DF DB) (1,0) / (3,0) / (5,5) / (0,3) / (1,-5) / (5,0) [5|13] |
第六步
| (1,0) / (6,6) / (-1,0) | / (6,0) / (6,0) / (6,0) | / (6,0) / (0,6) / (-1,-5) |
官方紀錄
| 世界紀錄 | 單次 | 5.00s | Vicenzo Guerino Cecchini | 巴西 | Schoolmark Open 2018 |
| 平均 | 6.73s | Vicenzo Guerino Cecchini | 巴西 | Schoolmark Open 2018 | |
| 中國記錄 | 單次 | 5.87s | 馮子甲 | 中國 | 2017WCA焦作魔方公開賽 |
| 平均 | 8.24s | 馮子甲 | 中國 | 2018WCA金華元旦魔方賽 |

