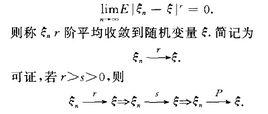r階平均收斂

通過隨機變數序列與其極限之差r階矩可以任意小來描述的收斂性，設r>0為常數，如果隨機變數ξ與ξ(n≥1)的r階矩皆有限，並且有limE|ξ-ξ|ʳ=0,則稱ξ為r階平均收斂到ξ，簡稱r階收斂，當r=1時可稱作平均收斂，當r=2時成為均方收斂，此時ξ稱作序列ξ的均方極限，這是均方隨機分析中使用的極限。

簡介

設有隨機變數列ξ₁，ξ₂，……，

r>0，E|ξ|ʳ<∞，和E|ξ|ʳ<∞，n=1，2，……

如果limE|ξ-ξ|ʳ=0

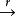r階平均收斂

那么，稱隨機變數列ξ₁，ξ₂，……，r階均值收斂（簡稱r-階收斂），並且收斂於隨機變數ξ，簡記作ξ ξ。

當r=1時稱為平均收斂。

當r=2時又叫均方收斂。

性質

r階收斂可歸納以下幾個性質：

性質1

r階平均收斂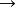

r階平均收斂

對於0<r<S，若ξ ξ，則ξ ξ。

性質2

如果對於某個r>0，隨機變數列ξ₁，ξ₂，……r階收斂於隨機變數ξ，則它一定也依機率收斂於ξ。

性質3

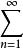r階平均收斂

對於某個r>0，有 E|ξ-ξ|ʳ<∞，則ξ以機率1收斂於ξ。