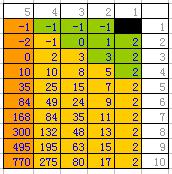
基本知識
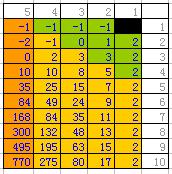高階等差數列⒈定義：一般地，如果{ a － a }是K階等差數列，就稱原數列{ a }為 K+1階等差數列，二階以及高於二階的等差數列統稱為高階等差數列。
⒉如果某數列的p階差數列是一非零常數列，則稱此數列為p階等差數列
⒊高階等差數列是二階或二階以上等差數列的統稱
⒋高階等差數列的性質：
⑴如果數列是p階等差數列，則它的一階差數列是p-1階等差數列
⑵數列是p階等差數列的充要條件是：數列的通項是關於n的p次多項式
⑶ 如果數列是p階等差數列，則其前n項和S是關於n的p+1次多項式
⒌高階等差數列中最重要也最常見的問題是求通項和前n項和，更深層次的問題是差分方程的求解，解決問題的基該方法有：
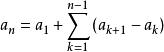高階等差數列⑴逐差法：其出發點是
⑵待定係數法：在已知階數的等差數列中，其通項an與前n項和Sn是確定次數的多項式（關於n的），先設出多項式的係數，再代入已知條件解方程組即得
⑶裂項相消法：其出發點是a能寫成a=f(n+1)-f(n)
⑷化歸法：把高階等差數列的問題轉化為易求的同階等差數列或低階等差數列的問題，達到簡化的目的
例題精講
例1.
數列的二階差數列的各項均為16，且a=a=10，求a
法一：
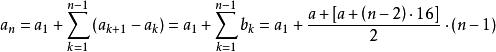高階等差數列顯然{ a}的二階差數列{ b}是公差為16的等差數列，設其首項為a，則b=a+(n-1）×16，於是
=a+(n-1)a+8(n-1)(n-2)
這是一個關於n的二次多項式，其中n2的係數為8，由於a=a=10，所以
a=8(n-63)(n-89)+10，從而a=8(51-63)(51-89)+10=3658
法二：
由題意，數列是二階等差數列，故其通項是n的二次多項式，又a=a=10，故可設a=A(n-63)(n-89)+10
由於是二階差數列的各項均為16，所以（a-a)-(a-a)=16
即a-2a+a=16，所以
A(3-63)(3-89)+10-2[A(2-63)(2-89)+10]+A(1-63）×（1-89)+10=16
解得：A=8
a=8(n-63)(n-89)+10，得a=8(51-63)(51-89)+10=3658
例2.
一個三階等差數列的前4項依次為30,72,140,240，求其通項公式
解：由性質⑵，a是n的三次多項式，可設a=A +B +C+D
由a=30、a=72、a=140、a=240得
A+B+C+D=30 A=1
8A+4B+2C+D=72 解得： B=7
27A+9B+3C+D=140 C=14
64A+16B+4C+D=240 D=8
所以a=n +7n +14n+8
例3.
求和：S=1×3×2 +2×4×3 +…+n(n+2)(n+1)
解：S是是數列{n(n+2)(n+1) }的前n項和，
因為a=n(n+2)(n+1) 是關於n的四次多項式，所以{ a}是四階等差數列，於是S是關於n的五次多項式
k(k+2)(k+1) =k(k+1)(k+2)(k+3)-2k(k+1)(k+2），故求S可轉化為求
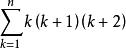高階等差數列
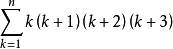高階等差數列K=和T=
高階等差數列k(k+1)(k+2)(k+3)=[ k(k+1)(k+2)(k+3)(k+4)-(k-1) k(k+1)(k+2)(k+3)]，所以
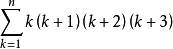高階等差數列
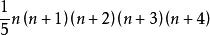高階等差數列K==
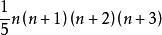高階等差數列 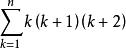高階等差數列T==
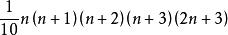高階等差數列從而S=K-2T=
例4.
已知整數列適合條件：
⑴a=3a-3a+a,n=2,3,4，…
⑵2a=a+a-
⑶a-a=9,a=1
求數列{ a}的前n項和S
解：設b=a-a,C=b-b
C=b-b= (a-a)-(a-a)=a-2a+a=(3a-3a+a) -2a+a=a-2a+a
=C (n=2,3,4，…）
所以{ C }是常數列
由條件⑵得C=2，則{ a}是二階等差數列
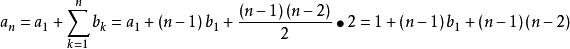高階等差數列因此
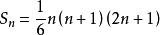高階等差數列由條件⑶知b=9，從而b=3，於是a=n ,
例5.
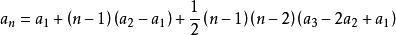高階等差數列求證：二階等差數列的通項公式為
證明：設{ a}的一階差數列為{ b}，二階差數列為{ c}，由於{ a}是二階等差數列，故{ c}為常數列
又c=b-b=a-2a+a
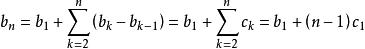高階等差數列
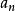高階等差數列
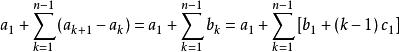高階等差數列所以=
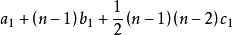高階等差數列=
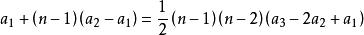高階等差數列=
例6.
求數列1,3+5+7,9+11+13+15+17，…的通項
解：問題等價於：將正奇數1,3,5，…按照“第n個組含有2n-1個數”的規則分組：
⑴、（3,5,7）、（9,11,13,15,17），… 然後求第n組中各數之和a
依分組規則，第n組中的數恰好構成以2為公差的項數為2n-1的等差數列，因而確定了第n組中正中央這一項，然後乘以（2n-1）即得a
將每一組的正中央一項依次寫出得數列：1,5,13,25，…這個數列恰為一個二階等差數列，不難求其通項為2n -2n+1，故第n組正中央的那一項為2n -2n+1，從而
a=(2n-2n+1)(2n-1)
例7.
數列{ a}的二階差數列是等比數列，且a=5,a=6,a=9,a=16，求{ a}的通項公式
解：易算出的二階差數列是以2為首項，2為公比的等比數列，則c=2 ,
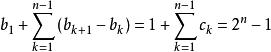高階等差數列的一階差數列設為b，則b=1且b=,
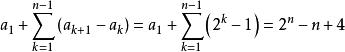高階等差數列從而an=
例8.
設有邊長為1米的正方形紙一張，若將這張紙剪成一邊長為別為1厘米、3厘米、…、（2n-1）厘米的正方形，恰好是n個而不剩餘紙，這可能嗎？
解：原問題即是是否存在正整數n，使得1 +3 +…+(2n-1) =100
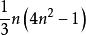高階等差數列 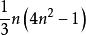高階等差數列 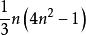高階等差數列由於1 +3 +…+(2n-1) =[1 +2 +…+(2n-1) ]-[2 +4 +…+(2n) ]=隨著n的增大而增大，當n=19時=9129<10000，當n=20時=10660>10000
故不存在…
例9.
對於任一實數序列A={a,a,a，…}，定義DA為序列{a-a,a-a，…}，它的第n項為a-a，假設序列D(DA）的所有項均為1，且a=a=0，求a
解：設序列DA的首項為d，則序列DA為{d,d+1,d+2，…},它的第n項是d+(n-1），因此序列A的第n項
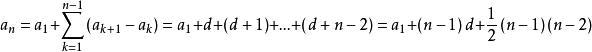高階等差數列
高階等差數列顯然a是關於n的二次多項式，首項等比數列為
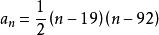高階等差數列由於a=a=0，必有
所以a=819
