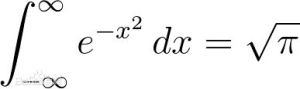基本介紹
高斯積分(Gaussian integral),有時也被稱為機率積分,是高斯函式(f(x) = e^{-x^2})的積分。它是依德國數學家兼物理學家卡爾·弗里德里希·高斯之姓氏所命名。
高斯積分求解
高斯積分在機率論和連續傅立葉變換等的統一化等計算中有廣泛的套用。在誤差函式的定義中它也出現。雖然誤差函式沒有初等函式,但是高斯積分可以通過微積分學的手段解析求解。
(Gaussian quadrature)
首先我們說明一下這裡使用積分的符號:
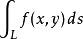 高斯積分
高斯積分表示f(x,y)在曲線L上的第一型曲線積分。
首先看第一型曲線積分形式的高斯積分:
設L是一條曲線,r是這曲線一點到L外一點A(e,m)的連線向量,n是曲線這一點的法向量,(r,n)表示r與n向量的夾角,則積分為:
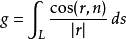 高斯積分
高斯積分d
高斯積分的幾何意義就是:
g是從點A所能看到曲線L的角的度量。
設(x,n)是x軸正方向與n的夾角,(x,r)是x軸正方向與r的夾角,則
(r,n) = (x,n) - (x,r)
所以
cos(r,n) = cos(x,n)cos(x,r)+sin(x,n)sin(x,r)
=((x-e)cos(x,n)/|r| + (y-m)sin(x,n)/|r|
代入高斯積分
g = ∫[L] ((y-m)sin(x,n)/(|r|^2) + (x-e)cos(x,n)/(|r|^2)) ds
化成第二型曲線積分
g = ±∫[L] ((y-m)/(|r|^2) dx - (x-e)/(|r|^2) dy)
±表示法線n的兩個方向。
此方程滿足積分路徑無關的條件,假如L是一條閉曲線,A在L外部,那么g=0,如果A在內部,根據挖奇點法,積分結果為2π。
其他相關
高斯積分公式:中國科學技術大學[引用日期2014-02-18]