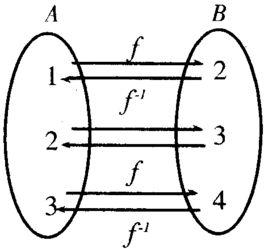
簡介
設f是從集合A到集合B的映射，若f(A)=B，即B中任一元素b都是A中某元素的像，則稱f為A到B上的 滿射；
若對A中任意兩個不同元素a(1)不等於a(2)，它們的像f<a(1)>不等於f<a(2)>，則稱f為A到B的 單射；
若映射f既是單射，又是滿射，則稱映射f為A到B的“雙射”(或“一一映射”)。 函式為雙射若且唯若每個可能的像有且僅有一個變數與之對應。
函式f: A → B為雙射若且唯若對任意b∈B存在唯一a∈A滿足f(a) = b。
函式f : A → B為雙射若且唯若其可逆，即，存在函式g: B → A滿足g o f = A上的恆等函式，且f o g為B上的恆等函式。
兩個雙射的複合也是雙射。如g o f為雙射，則僅能得出f為單射且g為滿射。
同一集合上的雙射構成一個對稱群。
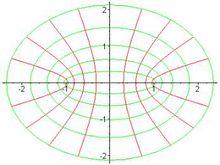映射函式如果X,Y皆為實數集 R，則雙射函式f: R→ R可以被視覺化為兩根任意的水平直線只相交正好一次。（這是水平線測試的一個特例。）
定義
在集合論中，一個由集合 X至集合 Y的映射稱為 雙射的，若對集合 Y內的任意元素 y，存在唯一一個集合 X內的元素 x，使得 y = f( x)。
換句話說， f為雙射的若其為兩集合間的 一對一對應，亦即同時單射且滿射。
例如，由整數集合至的函式succ，其將每一個整數 x連結至整數succ( x)=x+1，及另一函式sumdif，其將每一對實數( x, y)連結至sumdif( x, y) = ( x + y, x − y)。
一雙射函式亦稱為 置換。後者一般較常使用在 X= Y時。以由 X至 Y的所有雙射組成的集合標記為 X Y.
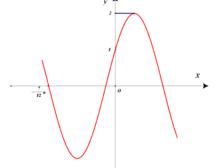三角函式圖像雙射函式在許多數學領域扮演著很基本的角色，如在同構(和如同胚和微分同構等相關概念)、置換群、投影映射及許多其他概念的基本上。
舉例
假設存在關於x的函式:y=2x+3，對於任何x∈R及y∈R，由於y是x的線性函式，因此對於任何x都有唯一確定的y與其對應。又通過整理可以得到x=(y-3)/2，因此對於任何y，也有唯一確定的x與其對應。這樣，在y=2x+3在x∈R、y∈R的域中就是一個雙射函式。
而對於函式y=x +2，對於x∈R、y∈R的取值範圍內，對於任何x，都有唯一確定的y與其對應。但對於
y≠2，任何y都對應2個不同的x。這樣y=x^+2在x∈R、y∈R的取值範圍內，不是雙射函式。但對於x∈[0,+∞）、y∈[2,+∞)。對於任何x，都有唯一確定的y與之對應，而對於任何y，都有x=(y-2)^0.5，即唯一確定的x與之對應。因此它是一個雙射函式。
套用
雙射的原理是一組關係，在判別某一種想法在套用能否雙向的找到某一唯一對應的事物，理論上通常要判斷這種想法是否滿足雙射的關係。因為具體的實施這一想法的途徑我們是並不知道的，所以需要抽象出他們的關係，找到這個雙射，如果找不到，並且驗證這個雙射不存在，那么想法是不可能實現的。
性質
（1）一由實數 R至 R的函式 f是雙射的若且唯若其圖像和任一水平線相交且只相交於一點。
（2）設 X為一集合，則由 X至其本身的雙射函式，加上其複合函式(0)的運算，會形成一個群，一個 X的對稱群，其標記為S( X)、 S X或 X!。
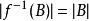雙射（3）取一定義域的子集 A及一陪域的子集 B，則| f( A)| = | A| 且。
（4）若 X和 Y為具相同勢的有限集合，且 f: X → Y，則下列三種說法是等價的：
f 為一雙射函式；
f 為一滿射函式；
f 為一單射函式。
區別
IoC的優點和缺點
IoC最大的好處是因為把對象生成放在了XML里定義，所以當我們需要換一個實現子類將會變成很簡單（一般這樣的對象都是實現於某種接口的），只要修改XML就可以了，這樣我們甚至可以實現對象的熱插撥（有點象USB接口和SCIS硬碟了）。
IoC最大的缺點是：（1）生成一個對象的步驟變複雜了（其實上操作上還是挺簡單的），對於不習慣這種方式的人，會覺得有些彆扭和不直觀。
（2）對象生成因為是使用反射編程，在效率上有些損耗。但相對於IoC提高的維護性和靈活性來說，這點損耗是微不足道的，除非某對象的生成對效率要求特別高。
（3）缺少IDE重構操作的支持，如果在Eclipse要對類改名，那么還需要去XML檔案里手工修改，這似乎是所有XML方式的缺憾所在。
雙射（bijection，即 bidirectional injection的簡稱）：當注出（outject）屬性數據時，視圖可以通過名稱找到它。在 postback 或者組件初始化時，數據被注入（inject）到一個組件中。雙射與傳統 IOC 的主要不同點在於，雙射使長期作用域中的組件可以引用短期作用域中的組件。可以進行這種連線是因為雙射在調用組件時（而不是啟動容器時）解析依賴項。雙射是有狀態組件開發的基礎。
雙射與勢
若 X和 Y為有限集合，則其存在一兩集合的雙射函式若且唯若兩個集合有相同的元素個數。確實，在公理集合論里，這正是“相同元素個數”的 定義，且廣義化至無限集合，並導致了基數的概念，用以分辨無限集合的不同大小。
