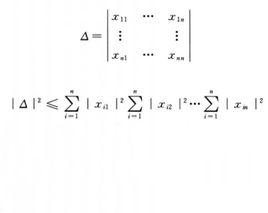基本介紹
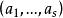 阿達馬不等式
阿達馬不等式對歐氏空間中任意s個向量 ,必有
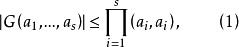 阿達馬不等式
阿達馬不等式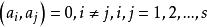 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式而等號成立的充要條件是: 。也即兩兩正交。(1)式稱為 廣義阿達馬不等式。
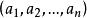 阿達馬不等式
阿達馬不等式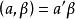 阿達馬不等式
阿達馬不等式之所以稱(1)式為廣義阿達馬不等式,是因為n階實方陣A= 的n個列可以看作帶有內積 的實數域R上的
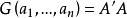 阿達馬不等式
阿達馬不等式n維列向量R (即歐氏空間R )中的n個列向量,而,故得
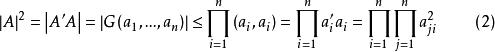 阿達馬不等式
阿達馬不等式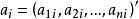 阿達馬不等式
阿達馬不等式(其中),這就是通常的 阿達馬不等式。
不等式(2)有以下幾何意義:
平行多面體的體積不超過兩個互補“面”的體積的乘積,而等於這一乘積的充分必要條件是這些“面”互相正交或者在乘積中至少有一個體積等於零 。
相關介紹
 阿達馬不等式
阿達馬不等式設是歐氏空間V中任意s個向量,下述s階陣
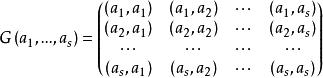 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式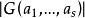 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式為的 格蘭姆矩陣。稱為的格蘭姆行列式 。
格蘭姆矩陣是個有廣泛套用的矩陣,它有如下的基本結論:
 阿達馬不等式
阿達馬不等式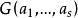 阿達馬不等式
阿達馬不等式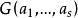 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式定理1 歐氏空間V中向量的格蘭姆矩陣必是半正定陣,而是正定陣的充要條件是線性無關。
 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式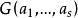 阿達馬不等式
阿達馬不等式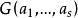 阿達馬不等式
阿達馬不等式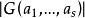 阿達馬不等式
阿達馬不等式證明 當線性無關時,作線性包L(),則它對V的內積來說仍是一個歐氏空間,而是L()的基,故是度量矩陣,因而是正定陣。故>0。
 阿達馬不等式
阿達馬不等式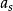 阿達馬不等式
阿達馬不等式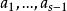 阿達馬不等式
阿達馬不等式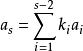 阿達馬不等式
阿達馬不等式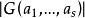 阿達馬不等式
阿達馬不等式當線性相關,例如是的線性組合:,將的第s列減去第1列的k倍、第2列的k倍、…,第s-1列的k倍,並套用內積的線性性質可得
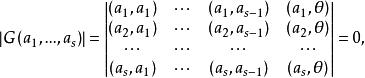 阿達馬不等式
阿達馬不等式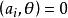 阿達馬不等式
阿達馬不等式(因;i=1,2,…,s)。
 阿達馬不等式
阿達馬不等式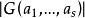 阿達馬不等式
阿達馬不等式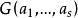 阿達馬不等式
阿達馬不等式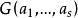 阿達馬不等式
阿達馬不等式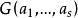 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式根據上述兩點,對任意s個向量,恆有:≥0。但因的任何k階主子陣顯然也是格蘭姆矩陣,故它的行列式不小於零,所以是半正定陣。再由上述兩點知,是正定陣的充要條件是,線性無關。
由定理1的證明過程,可得推論1及廣義阿達馬不等式。
 阿達馬不等式
阿達馬不等式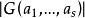 阿達馬不等式
阿達馬不等式 阿達馬不等式
阿達馬不等式推論1 歐氏空間V的任意s個向量的格蘭姆行列式≥0,而等號成立的充要條件是,線性相關。
由於格蘭姆矩陣的半正定(正定性),使我們可以充分運用半正定陣與正定陣的理論去得到更多有用的結論。例如,由正定陣行列式的不等式估計式顯然可得廣義阿達馬不等式 。