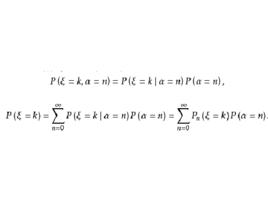基本介紹
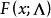 複合分布
複合分布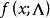 複合分布
複合分布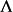 複合分布
複合分布複合分布是由分布參數的隨機化產生的機率分布。設隨機變數的分布函式[或機率函式]所依賴的參數本身是隨機變數,則由分布函式[或機率函式]
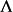 複合分布
複合分布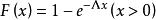 複合分布
複合分布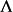 複合分布
複合分布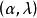 複合分布
複合分布所決定的機率分布稱做 複合分布。如X服從參數為的指數分布,其分布函式為,而服從參數為的分布,則相應的複合分布的分布函式為
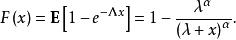 複合分布
複合分布混合分布也可以視為複合分布。
相關定理
設隨機變數服從的分布與一個參數有關,而也是一個隨機變數,它服從一個確定的分布,且與相互獨立,這時稱隨機變數服從一個複合分布 。
定理1設隨機變數與參數均是取值為非負整數的離散型隨機變數,且,則複合分布為
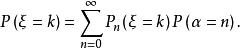 複合分布
複合分布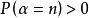 複合分布
複合分布證明:考慮二維隨機變數,對於,由條件分布,得
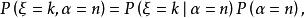 複合分布
複合分布故邊際分布
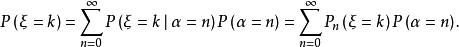 複合分布
複合分布即為所求。
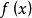 複合分布
複合分布定理2設為離散型隨機變數,為連續型隨機變數,其密度函式滿足,當
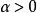 複合分布
複合分布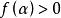 複合分布
複合分布時,時,,則複合分布為
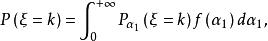 複合分布
複合分布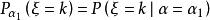 複合分布
複合分布其中。
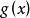 複合分布
複合分布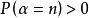 複合分布
複合分布定理3設為連續型隨機變數,其密度函式為,為離散型隨機變數,其分布滿足,則複合分布為
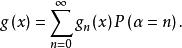 複合分布
複合分布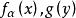 複合分布
複合分布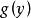 複合分布
複合分布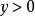 複合分布
複合分布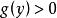 複合分布
複合分布定理4設,均為連續型隨機變數,其密度函式分別為且滿足,當時,,則複合分布的密度函式為
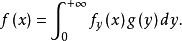 複合分布
複合分布舉例說明
例1 複合二項分布
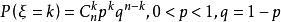 複合分布
複合分布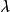 複合分布
複合分布設服從二項分布,,其中n服從參數為的泊松分布,則複合二項分布為
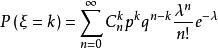 複合分布
複合分布 複合分布
複合分布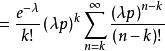 複合分布
複合分布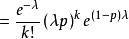 複合分布
複合分布例2 設隨機變數服從泊松分布
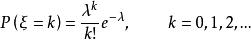 複合分布
複合分布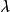 複合分布
複合分布其中參數是一個連續型隨機變數。其密度函式
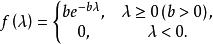 複合分布
複合分布則複合分布為
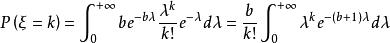 複合分布
複合分布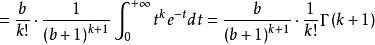 複合分布
複合分布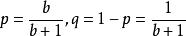 複合分布
複合分布令,,於是
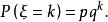 複合分布
複合分布