簡介
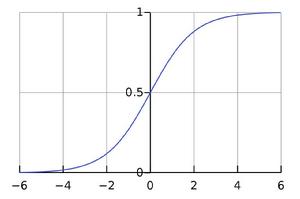
邏輯函式或 邏輯曲線是一種常見的S函式，它是皮埃爾·弗朗索瓦·韋呂勒在1844或1845年在研究它與人口增長的關係時命名的。廣義Logistic曲線可以模仿一些情況人口增長（P）的S形曲線。起初階段大致是指數增長；然後隨著開始變得飽和，增加變慢；最後，達到成熟時增加停止。
一個簡單的Logistic函式可用下式表示：
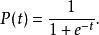羅吉斯蒂克函式邏輯差分方程
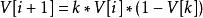羅吉斯蒂克函式
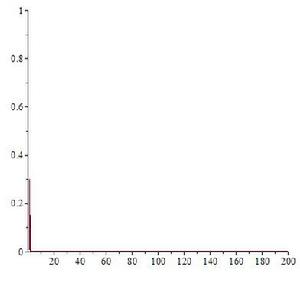
羅吉斯蒂克函式是混沌理論研究的一個課題這個函式對初始值和參數的變化很敏感，往往微小的變化會引起混沌。如圖所示，當V[1]=0.3，參數k 從0.1 變到 4 時，系統變化很大。
•當 k 由 0.1 變到 1 時， 曲線很快趨向於0；
•當 k 繼續增加，曲線由 0.3 上升到 一個穩定值；
•k 繼續增加 ，曲線出現擺動，有2個穩定值；
•k 繼續增加 ， 曲線相繼出現 4個、8個、16個32個....穩定值；
•k 增加到一個臨界值，系統進入混沌狀態；
•K 再增加，系統突然垮塌。 [2]
參見
•廣義Logistic曲線
•龔配子氏曲線
•創新擴散理論
•拐點 (社會學)
•轉移Gompertz分布
•哈伯特曲線
•Logistic分布
•Logistic映射
•Logistic回歸
•Logit
•對數似然比
•馬爾薩斯增長模型
•r/K選擇理論
•Logistic平滑轉換模型
•希維賽德階躍函式
