絕對穩定性

非線性特性可在一個限制類中任意選取時的非線性反饋系統的穩定性。絕對穩定性和通常意義下的穩定性很不相同。

正文

絕對穩定性研究在某種限制下的一類非線性系統為全局漸近穩定的條件，而通常意義下的穩定性則只局限於對具體的非線性系統個別進行分析。非線性反饋系統（見圖）是反饋控制系統的一種類型，它的特點是：前饋通道中的部件是線性的，用傳遞函式G(s)來描述；反饋通道中的部件具有非線性特性，表示為 σ＝嗘(y)。在工程問題中，一些快速控制系統常採用這種結構形式。在絕對穩定性的研究中,非線性特性的限制類常取為滿足不等式 k1y2≤y嗘(y)≤k2y2的所有非線性函式嗘(y)，其中k1和k2為常數。在k1和k2 給定後，絕對穩定性只依賴於線性部件的傳遞函式G(s)。研究絕對穩定性的方法主要有時間域的李雅普諾夫函式法和頻率域的波波夫法。
時間域的李雅普諾夫函式法　先由線性部分的傳遞函式G(s)定出相應的狀態方程和輸出方程(見最小實現)

式中x為狀態，y為輸出,u為控制，v為參考輸入，A、B和C為相應的係數矩陣。隨後,取李雅普諾夫函式（見李雅普諾夫穩定性理論）為

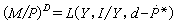
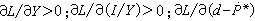
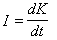式中xT為x的轉置，L為正定對稱矩陣，β取為使得V(x)對任意非零的x均為正值。系統絕對穩定性的判據表明，如果李雅普諾夫函式V(x)在系統狀態方程的約束下對時間t的全導數當x≠0時均為負值,那么非線性反饋系統是絕對穩定的。
頻率域的波波夫法　對於給定的線性部分傳遞函式G(s)，取s=j&owega;可得頻率回響G（j&owega;）,並構造輔助函式

式中ReG（j&owega;）和ImG（j&owega;）分別表示G（j&owega;）的實部和虛部,&owega;為頻率。波波夫判據可表示為：對於非線性反饋系統，如果非線性特性嗘(y)滿足不等式0≤y嗘(y)≤ky2(k>0)所規定的限制,並且存在有限實數q，使對一切&owega;值下式成立：

則系統的零平衡狀態是全局漸近穩定的。
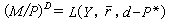
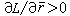
不管是李雅普諾夫函式法還是波波夫法都只給出判斷絕對穩定性的充分條件。不符合判據條件的系統仍然有可能是絕對穩定的。而且，李雅普諾夫函式法和波波夫法實質上是等價的。

配圖

相關連線