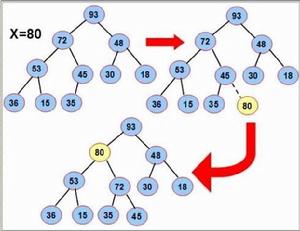
簡介
令U為無向圖G的頂點的子集,若且唯若對於U中的任意點u和v,(u , v)是圖G的一條邊時,U定義了一個完全子圖(complete subgraph)。子圖的尺寸為圖中頂點的數量。若且唯若一個完全子圖不被包含在G的一個更大的完全子圖中時,它是圖G的一個完備子圖。最大的完備子圖是具有最大尺寸的完備子圖。
最大完備子圖問題
如果U定義了G的一個完全子圖,則它也定義了的一個空子圖,反之亦然。所以在G的完備子圖與的獨立集之間有對應關係。特別的,G的一個最大完備子圖定義了的一個最大獨立集。
最大完備子圖問題是指尋找圖G的一個最大完備子圖。類似地,最大獨立集問題是指尋找圖G的一個最大獨立集。這兩個問題都是N P-複雜問題。當用算法解決其中一個問題時,也就解決了另一個問題。例如,如果有一個求解最大完備子圖問題的算法,則也能解決最大獨立集問題,方法是首先計算所給圖的補圖,然後尋找補圖的最大完備子圖。
算法思想
定義一個圖,圖中每個頂點表示一個網組。若且唯若兩個頂點對應的網組交叉時,它們之間有一條邊。所以該圖的一個最大獨立集對應於非交叉網組的一個最大尺寸的子集。當網組有一個端點在路徑頂端,而另一個在底端時,非交叉網組的最大尺寸的子集能在多項式時間(實際上是(n))內用動態規划算法得到。當一個網組的端點可能在平面中的任意地方時,不可能有在多項式時間內找到非交叉網組的最大尺寸子集的算法。
最大完備子圖問題和最大獨立集問題可由回溯算法在O (n2)時間內解決。兩個問題都可使
用子集解空間樹。考察最大完備子圖問題。當試圖移動到空間樹的i層節點Z的左孩子時,需要證明從頂點i到每一個其他的頂點j(xj= 1且j在從根到Z的路徑上)有一條邊。當試圖移動到Z的右孩子時,需要證明還有足夠多的頂點未被搜尋,以便在右子樹有可能找到一個較大的完備子圖。
C++算法示例
回溯算法可作為類AdjacencyGraph的一個成員來實現,為此首先要在該類中加入私有靜態成員x(整型數組,用於存儲到當前節點的路徑),b e s t x(整型數組,保存目前的最優解),b e s t n(b e s t x中點的數量),c n(x中點的數量)。所以類AdjacencyGraph的所有實例都能共享這些變數。
函式maxClique是類AdjacencyGraph的一個私有成員,而MaxClique是一個共享成員。函式maxClique對解空間樹進行搜尋,而MaxClique初始化必要的變數。MaxClique( v )的執行返回最大完備子圖的尺寸,同時它也設定整型數組v,若且唯若頂點i不是所找到的最大完備子圖的一個成員時,v [ i ] = 0。
最大完備子圖