簡介
施凱特 p 類運算元是緊運算元中重要的子類。
施凱特p類運算元設H是可分的希爾伯特空間，(H)是H上的緊運算元全體，對於 T (H)
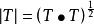施凱特p類運算元
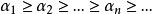施凱特p類運算元也是緊的，設其特徵值按大小順序為 （按重複度重複編號）p>0,(H) 中滿足
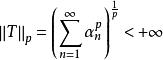施凱特p類運算元全體記為 C(H) ，簡記為C，稱為 H 上的施凱特 p 類。
推論
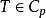施凱特p類運算元
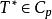施凱特p類運算元
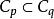施凱特p類運算元若 ，則 。當 1≤p<q，則 。若p,q,r滿足
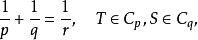施凱特p類運算元
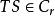施凱特p類運算元則 。
特別重要的是p=1,2的情形。C和C類運算元分別稱為跡類運算元和希爾伯特-施密特運算元，而相應的範數‖·‖和‖·‖分別稱為跡範數和希爾伯特-施密特範數。
性質
設{e}是H的規範正交基，當T∈C時，T的跡tr(T)定義為
施凱特p類運算元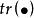
施凱特p類運算元
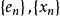施凱特p類運算元（此級數絕對收斂，其值不依賴基的選取）， 都是巴拿赫空間C上的連續線性泛函。設 都是 H 的規範正交基，則
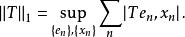施凱特p類運算元
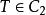施凱特p類運算元當 時，
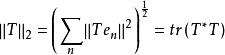施凱特p類運算元
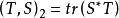施凱特p類運算元
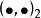施凱特p類運算元在C中可定義內積 ，則C按 成為希爾伯特空間。
