簡介
振幅函式是關於任意多重指標的偏導數滿足某種類型不等式的函式。
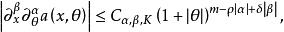 振幅函式
振幅函式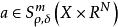 振幅函式
振幅函式設X是R 中開子集,0≤ρ,δ≤1,m為任意實數。若函式a(x,θ)∈C (X×R )滿足如下條件:對任意多重指標α,β及X中的緊集K,存在常數C,使當x∈K,θ∈R 時有則稱a(x,θ)是m次(ρ,δ)型振幅,記為。
發展
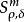 振幅函式
振幅函式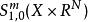 振幅函式
振幅函式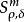 振幅函式
振幅函式振幅函式類首先由赫爾曼德爾(Hormander,L.V.)引進。從歷史上看,最古典的振幅函式類是其中函式a(x,θ)∈C (X×R )關於θ為m次齊次函式(它顯然屬於。)而赫爾曼德爾所引入的上述,其主要特色在於用微分不等式代替了齊次性。
振幅函式類
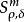 振幅函式
振幅函式類是較為典型的振幅函式類。而在處理具體問題時,將出現一些新的特殊的振幅函式類,並且還要對它們建立一套與相應的運算元相配合的運算規則以及相應的振盪積分理論等。
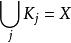 振幅函式
振幅函式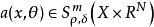 振幅函式
振幅函式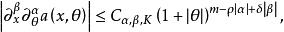 振幅函式
振幅函式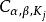 振幅函式
振幅函式取X中的上升緊集序列{K}使。對於,記使微分不等式成立的最小常數為ρ[a]。
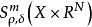 振幅函式
振幅函式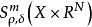 振幅函式
振幅函式易知它們構成一個可分離的可列半模族,且用它裝備函式類後使得成為一個弗雷歇空間。
漸進展開形式
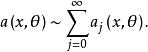 振幅函式
振幅函式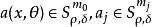 振幅函式
振幅函式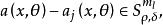 振幅函式
振幅函式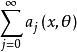 振幅函式
振幅函式一般地,振幅函式常取漸近展開的形式:具體地,設{m}(j=0,1,2,...)是一個單調下降趨於-∞的實數列。又設,若對任意非負整數l有則稱是a(x,θ)的漸近展開。
