循環褶積

循環褶積是兩個給定的序列分別延拓為周期性序列後，按周期褶積原理對其進行運算，結果也是一個周期性序列。如果僅取其一個周期內的結果，就得到循環褶積的序列。

循環褶積

設有兩個長度均為N的序列x(n)和h(n)進行褶積，先將它們經周期延拓變為周期序列慜(n)和愢(n)，即

慜(n+kN)＝慜(n)　 愢(n+kN)＝愢(n)　0≤n≤N

式中k為任意整數，序列x(n)和h(n)可以分別看作周期序列慜(n)和愢(n)在一個周期內的主值序列。
x(n)和h(n)的循環褶積定義為

y(n)＝x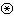(n)n(n)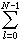＝x(l)n(n-l)NRN(n)
n＝0，1，2，…，N-1

其中RN(n)是矩形序列

RN(n)＝

nN是餘數運算表達式，它表示n對N 求餘數。
循環褶積的計算過程　現舉例說明循環褶積的計算過程。例如，兩個有限長度序列同為矩形序列

x(n)＝n(n)＝

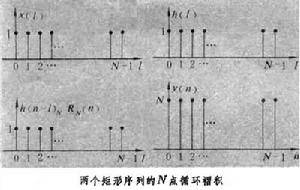這兩個矩形序列的N點循環褶積見圖。這個褶積過程可以理解為序列x(n)分布在N等分的圓筒壁上,而序列h(n)經卷褶後也分布在另一個N等分的同心圓筒壁上,每當兩個圓筒停在一定的相對位置時，兩個序列相乘求和即得褶積序列中的一個值。然後將一個圓筒相對於另一個圓筒旋轉移位，依次在不同位置下相乘求和，就得到全部褶積序列。由於序列h(n)是等值的，所以x(n)旋轉時,乘積x(l)h(n-l)的和總是等於N。

循環褶積

如果兩個序列x(n)和h(n)的長度分別為N和M，設x(n)代表信號序列,h(n)代表線性系統的衝激回響序列，則要求系統輸出是線性褶積

y(n)＝x(n)*h(n)

為了從它們的循環褶積得到線性褶積而不發生序列交疊的混淆現象，要將兩序列的長度各擴長為L≥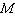+N-1,即x(n)只有前N個非零值,後L-N個均為補充的零值;而h(n)只有前M個是非零值,後L-M個均為補充的零值。由此求循環褶積，其結果就等於兩序列的線性褶積。
用快速傅立葉變換計算循環褶積,當N 較大時,直接計算循環褶積的運算量相當大。因此，有必要尋求簡便、快速計算循環褶積的變換方法。為此，所用變換的快速結構必須具有若干良好的性質。
①循環褶積性，即兩個序列的循環褶積的變換等於它們各自變換的乘積；
②變換是可逆的；
③變換是線性的。滿足上述性質的變換方法有傅立葉變換、數論變換等。
當採用快速傅立葉變換(FFT)技術求解褶積時,兩個時域序列的循環褶積的離散傅立葉變換 (DFT)等於它們的離散傅立葉變換之乘積，即

Y(k)＝DFT【x(n)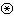n(n)】＝X(k)H(k)

對Y(k)求離散傅立葉反變換(IDFT)，即可得到兩個序列的循環褶積

y(n)＝IDFT【Y(k)】

由上述計算過程可看出，直接褶積所需乘法運算次數為N2，利用FFT算法計算循環褶積共需要三次FFT運算（計算IDFT所需乘法次數與計算DFT的相同）與N 次乘法,總共需要乘法次數為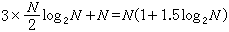

所以,N 越長,利用快速變換算法計算循環褶積的優越性越大。通常將循環褶積也稱為快速褶積。
參考書目
　何振亞著：《數位訊號處理的理論與套用》上冊，人民郵電出版社，北京，1983。
　A. V. Oppenheim, R. W. Schafer, Digital Signal Processing, Prentice Hall, Inc., Englewood Cliffs,New Jersey,1975.

配圖

相關連線