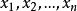 平均值不等式
平均值不等式設 為n個正數,則其算術平均值不小於其幾何平均值,即
n個正數的算術平均值與幾何平均值的比較。
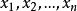 平均值不等式
平均值不等式設 為n個正數,則其算術平均值不小於其幾何平均值,即
算術-幾何平均值不等式,簡稱算幾不等式,是一個常見而基本的不等式,表現了算術平均數和幾何平均數之間恆定的不等關係。
介紹 證明 例子 推廣 參見設ai
一般形式 加權形式 證明簡述內容介紹《平均值不等式與柯西不等式》主要介紹平均值不等式和柯西不等式...夫不等式和閔可夫斯基不等式,內容豐富、全面。重點介紹了平均值不等式與柯西不等式在證明不等式和求最值等問題中的套用。《平均值不等式與柯西不等式》所...
內容介紹平均數不等式,或稱平均值不等式、均值不等式,是數學上的一組不等式,也是基本不等式的推廣。
定義 證明方法 參見楊氏不等式又稱Young不等式 ,Young不等式是加權算術-幾何平均值不等式的特例,Young不等式是證明Holder不等式的一個快捷方法。
一般形式 加權形式 證明集中不等式是數學中的一類不等式,描述了一個隨機變數是否集中在某個取值附近。 例如大數定律說明了一系列獨立同分布隨機變數的平均值在機率上趨近於它們的數學期...
馬爾可夫不等式 切比雪夫不等式卡萊曼不等式(Carleman inequality)是關於項為乘積冪的級數的估計式及其推廣,這個不等式由卡萊曼(T.Carleman)於1923年發表 。
基本介紹 卡萊曼不等式的證明卡爾松不等式(Carlson)往往也被稱為矩陣長方形不等式。是由里納特·卡爾松發現提出的。外文名又叫做Carlson,是數學上的著名不等式之一。
內容表述 數學證明在機率論中,馬爾可夫不等式給出了隨機變數的函式大於等於某正數的機率的上界。雖然它以俄國數學家安德雷·馬爾可夫命名,但該不等式曾出現在一些更早的文獻中,其...
簡介 矩陣形式 套用實例