分類
希爾伯特R樹有兩種：一種是提供給靜態資料庫，還有一種是提供給動態資料庫。在這兩種情況下，希爾伯特的填充曲線都是用來使結點上的多維數據對象獲得一個更好的排序。要把一個排序稱為“好排序”，從某種意義上來說，它需要將“相似或相近”的數據矩形聚集在一起並使該矩形的面積和最小邊界矩形或最小外接矩形（MBRs）結果的周長達到最小。緊縮的希爾伯特R樹（Packed Hilbert R-trees）在很少進行數據更新甚至從不需要進行數據更新的靜態資料庫中顯得非常的適用。
動態的希爾伯特R樹 則適用於插入、刪除、更新這些操作發生非常頻繁的動態資料庫。此外，動態希爾伯特R樹採用靈活的延遲的分裂機制來提高空間利用率。每一個結點都有定義明確的一組兄弟結點集合。通過調整分裂的策略，希爾伯特R樹可以使其空間利用率達到人們所期望的那樣高。因此，在R樹結點上提出一種排序，我們便可以達到上述目的。希爾伯特R樹（如，最小邊界矩形等）依照矩形中心的希爾伯特值來對矩形進行排序。（某一個點的希爾伯特值是從原點到該點的希爾伯特曲線長度）。考慮到這個排序，每一個結點都有一組定義明確的兄弟結點；因此，延遲分裂技術可以被使用。通過調整分裂策略，希爾伯特R樹可以獲得一個人們所期望的高利用率。相反，其他的R樹變體沒有在空間利用率上加以控制。
基本思想
儘管下面這個例子是在一個靜態的環境下，但是他還是可以將一個好的R樹設計原理直觀的展現出來。這些原理對靜態和動態資料庫都有效。
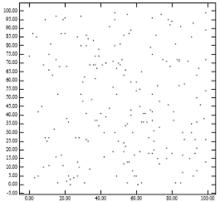圖1-1：200個獨立分散的點數據Roussopoulos和Leifker兩個人提出了一種構造一個緊縮的R樹的方法，幾乎可以使R樹的空間利用率達到100%。這個想法就是在矩形的一個角的x坐標或者y坐標上來進行數據的排序。從四個角建立坐標系來使數據排序的結果基本一致。在下面的討論中，我們從左下角開始按x軸來對數據進行排序，我們稱這種排序成為“低x軸緊縮R樹”（lowx packed R-tree）。排序好的矩形序列通過掃描之後，連續的矩形被分到同一個葉結點直到該結點被填滿，然後我們就創建一個新的葉結點，對已排序的序列掃描繼續執行。因此，最後生成的R樹的葉結點都會被緊密地填滿，不過每一層的最後一個節點有可能發生異常。這樣空間利用率基本就可以達到100%。這棵樹的更高層的生成方式與此相同。
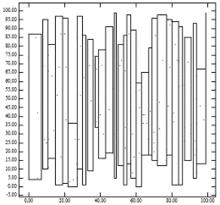圖1-2：通過“低x軸緊縮R樹”算法生成的結點的最小邊界矩陣圖1-1突出了低x軸緊縮R樹的問題。圖1-1為我們需要建立R樹的所有點的示意圖。圖1-2展示了以圖1-1中展示所有點為基礎按照低x軸緊縮方法將會產生的R樹的葉結點。可以看出父結點僅僅覆蓋了一個很小的區域，這一事實解釋了為什麼低x軸緊縮R樹在點查詢上有著如此優異的性能。然而，父親結點有著非常長的周長解釋了區域查詢時性能降低的情況。這一結果與R樹性能的解析方程的結果一致。我們可以直觀的看出，緊縮算法應該把附近的點分配到同一葉結點。低x軸緊縮R樹忽視了y軸，這也在某種程度上違反了這個經驗法則。
下面一節描述了兩種希爾伯特R樹的變體。第一種適用於數據更新很少或者基本不更新的靜態資料庫。最後生成的R樹的葉結點都會被緊密地填滿，不過每一層的最後一個節點有可能發生異常。這樣空間利用率基本就可以達到100%。這種方法被稱為緊縮型希爾伯特R樹（Packed Hilbert R-tree）。第二種被稱為動態希爾伯特R樹，它支持在動態的環境中進行插入刪除等操作。
緊縮型希爾伯特R樹
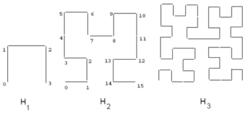圖2：1階、2階、3階希爾伯特曲線下面對希爾伯特曲線進行一個簡短的介紹。最基本的希爾伯特曲線是在一個2×2的格線中，在圖2中用H來表示。為了衍生出i階曲線，我們需要用i-1階曲線來替代每一個在基本曲線上的頂點，不過在有些地方需要進行適當的旋轉或對稱。圖2中同樣的展示了二階和三階希爾伯特曲線。當希爾伯特曲線趨近於無窮大階，就像其他空間填充曲線一樣，所得到的曲線就是一種分形 （fractal），其分形維數為2 。希爾伯特曲線可以被推廣到更高維。如何以一個給定的順序畫二維分形曲線在 和 中可以找到相關算法。更高維的算法在 中給出。
空間填充曲線的路徑給格點附加了一個線性的順序；我們可以這樣來建立這條路徑，從一個端點開始沿著曲線直到曲線的另一個端點。每一個點的實際坐標值也就可以被計算出來。然而對於希爾伯特曲線這一數值比z型曲線要難計算得多。圖2中還展示了一個4×4格線中的順序（見曲線H）。舉個例子，點(0,0)在H上有希爾伯特值0，而點(1,1)有希爾伯特值2。一個矩形的希爾伯特值通過矩形中心的希爾伯特值來表示。
希爾伯特曲線給數據矩形附加了一個線性順序然後貫穿整個已排序的序列，並且將每一個包含C個矩形的集合分配到R樹上的一個結點。最終的結果就會是在同一個結點上的數據矩形集合中的所有矩形和同一結點上其他矩形線上性順序上都非常的相近，很有可能就是相鄰的空間；因此，生成的R樹結點的區域就會非常小。圖2說明了為什麼我們的以希爾伯特曲線為基礎的結果會有一個非常好的性能的直觀原因。我們所利用的數據是由很多點組合而成（和圖一中所給的點相同）。如果我們按照希爾伯特值對這些點進行分組，所產生的的R樹結點的最小邊界矩陣就會趨向於小的類似於正方形的矩形。這就告訴我們結點就很有可能有小的面積和周長。面積值小意味著點查詢性能優異，面積和周長都小則會在大型的查詢中有著優異的表現 。
希爾伯特緊縮算法
Hilbert-Packing
（將矩形封裝成一棵R樹）
步驟一：計算每一個數據矩形的希爾伯特值
步驟二：按照希爾伯特值升序將數據矩形排序
步驟三：/*構造葉結點（層l=0）*/
while（有更多的矩形）
生成一個新的R樹結點
將後續C個矩形分配到這個結點上
步驟四：/*構造更高層（l+1）的結點*/
while（l層中不止1個結點）
把在層數I≥0上的結點按照創造時間的升序排列
重複步驟三
這裡，我們假設數據是靜態的或者產生變化的頻率很低。這對構造一個有接近100%的空間利用率並且有一個很好的回響時間的R樹有一定的簡單啟發。
動態希爾伯特R樹
一個矩形的希爾伯特值一般用其中心點的希爾伯特值來定義。
樹形數據結構
希爾伯特R樹有著如下的結構。一個葉結點包含了最多C個元素，在每一個表單（R,obj_id）中C是葉結點的容量，R是最小邊界矩形的實際對象(xx,y,y),obj_id是一個指向對象描述記錄的指針。
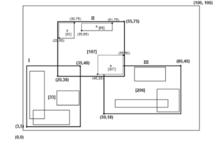圖3：希爾伯特R樹中的數據矩形
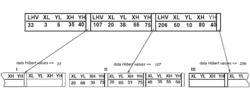圖4：希爾伯特R樹的檔案結構希爾伯特R樹和R*樹相比 ，最大的不同就是非葉結點中同樣包含了關於最大的希爾伯特值（LHV（Largest HilbertValue））的信息。因此，希爾伯特R樹的非葉結點包含至多個表單項（R,ptr,LHV）這其中，是非葉結點的容量，R是包含該結點所有子結點的最小邊界矩形，ptr是指向子結點的指針，LHV則是R中包含的數據矩形中的最大希爾伯特值。注意到當非葉結點從其子結點中挑選一個希爾伯特值作為它的LHV，這樣當計算非葉結點的最小邊界矩形的希爾伯特值時就不需要花費額外的代價。圖3表示了採用希爾伯特R樹中的一些矩形。x符號附近的數字即為矩形中心的希爾伯特值（僅僅在父結點中標出）。LHV則在方括弧中標出。圖4則展示了圖3是如何存儲在磁碟上的，父結點中的內容表現的更加詳細。在結點I中的數據矩形都有著一個的希爾伯特值；相似度結點中都有著一個的希爾伯特值，以此類推。
一個普通的R樹在結點溢出的時候分裂結點，從一個原始的結點中分出兩個新的結點。這種方法被稱為“一分為二”分裂法。同樣可以延遲分裂，等待至兩個結點分裂成三個結點，這和B*樹的分裂方法類似。這種方法被稱為“二分為三”方法。
通常來說，這種方發可以被推廣成“s分為s+1”分裂法。這裡s被稱為分裂方法的階。為了實現s階分裂方法，溢出的結點就會將該結點中的一些對象轉移到s-1個兄弟結點中，若他的兄弟結點都被填滿了，則執行“s分為s+1”操作。s-1個兄弟結點被稱為協作兄弟結點。
接下來，要介紹的是搜尋，插入還有溢出管理的詳細算法。
搜尋
搜尋算法和R樹變體中的相似，都是從根開始，逐級向下檢查所有的與待查找矩形相交的所有結點。在葉結點層，所有與查詢窗w相交的元素都被稱為有效數據項。
搜尋算法
Search(node Root, rect w):
S1. 查找非葉結點：
搜尋出所有最小邊界矩形與查詢窗w相交的項目
S2. 查找葉結點：
插入
在希爾伯特R樹上插入一個新的矩形r的時候，我們採用其中心的希爾伯特值h作為鍵值。在每一層中，我們選擇符合最小的LHV值都比h大這一條件的所有兄弟結點。當到達一個葉結點時，我們便根據h來講該矩形r插入到其正確的順序中。當一個矩形被插入到結點N後，我們採用 AdjustTree的算法來修正其上層所有結點的最小邊界矩形和最大希爾伯特值。
插入算法
Insert(node Root，rect r):
/*在希爾伯特R樹上插入一個新的矩形r。h是它的希爾伯特值*/
I1.尋找最優葉結點：
調用 ChooseLeaf(r,f)來選擇一個葉結點L放置矩形r
I2.在葉結點L中插入r：
if(L有空位)
在L中按照希爾伯特順序將r插入到一個合適的位置並返回
if(L已滿)
調用 HandleOverflow(L,r),必要的話會分裂出一個新的葉結點並返回
I3.向上傳遞變化：
構造一個包含L和他的協作兄弟結點還有新產生的葉結點（如果有的話）的集合S
調用 AdjustTree(S)
I4:拓展樹
如果分裂傳遞導致根結點分裂，構造一個新的根結點，它的子結點就是剛剛分裂成的兩個結點
ChooseLeaf算法
ChooseLeaf(rect r,int h):
/*返回放置矩形r的葉結點*/
C1.初始化：
把N設定為根結點
C2.檢查葉結點：
if(N是葉結點)
返回N
C3.選擇子樹：
if(N是非葉結點)
選擇有比h大的最小LHV值的元素 entry(R,ptr,LHV)
C4.向下查找直到到達葉結點：
把找到的結點的ptr指針設定為N，並且循環C2，C3，C4
AdjustTree算法
AdjustTree(set S):
/*S是包含更新的結點，它的協作兄弟結點（如果發生了溢出）還有新產生的結點NN（如果發生了結點分裂）。程式從葉結點向上執行到根結點，不斷調整包含了S中任一結點的結點的最小邊界矩陣MBR和最大希爾伯特值LHV。如果可能的話，它會傳遞分裂。*/
A1.if(到達了根結點)
停止
A2.向上傳遞分裂：
假設Np是結點N的父結點
if(N發生了分裂)
令新結點為NN
if(Np中有空間)
根據其希爾伯特值將NN以正確的順序插入到Np中
else
調用 HandleOverflow(Np,NN)
if(Np發生分裂)
令新結點為PP
A3.在其父結點層上調整MBR和LHV：
令P為S中結點的父結點集合
適當調整P中對應結點的MBR值和LHV值
A4.上移一層：
令P中各結點的父結點集合為S，如果Np分裂了的話令NN=PP
循環A1，A2，A3，A4
刪除
在希爾伯特R樹中，如果一個結點沒有父結點時，我們不需要在其父結點下溢時，將其重新插入樹中。取而代之的是我們可以借用其兄弟結點或者與兄弟結點合併的下溢結點的鍵值作為該結點的鍵值，因為這些結點有著很清楚的順序（根據最大希爾伯特值排序）；相反，在R樹中，我們沒有與兄弟結點相關的類似概念。值得注意的是刪除操作需要s個協作兄弟結點，但是插入操作則只需要s-1個兄弟結點。
刪除算法
Delete(r):
D1.找到主葉結點：
通過一個精確的匹配算法找到包含r的葉結點L
D2.刪除r：
把r從L中刪除
D3.
if(L下溢)
將s個協作兄弟結點中的一部分元素轉移到L中
if(所有的兄弟結點都即將要下溢)
把s+1個結點合併為s結點，並調整其他相關結點
D4.調整父結點層的MBR和LHV：
令S為包含L和其協作兄弟結點（如果發生了下溢）的集合
調用 AdjustTree(S)
上溢出控制
希爾伯特R樹中上溢出控制算法中對待上溢出結點有兩種方法，其一為將其一部分元素移至s-1號兄弟協作結點中，其二為將s個結點分裂成s+1個結點。
HandleOverflow算法
HandleOverflow(node N,rect r):
/*如果發生分裂，返回新結點*/
H1.令ε為包含N中所有元素及其s-1個協作兄弟結點的集合
H2.把r加入到ε中
H3.
if(s-1個協作兄弟結點中有一個未充滿)
根據希爾伯特值將ε中元素均勻分到s個結點中
H4.
if(所有s個協作兄弟結點都被充滿)
生成一個新的結點NN並根據希爾伯特值把ε中元素均勻分到s+1個協作兄弟結點中
返回NN
