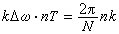射影測度

射影測度，1853年E.N.拉蓋爾將角度的度量概念與交比的射影性質聯繫起來，是利用射影幾何學的觀點解釋角度的一個重要嘗試。

射影測度

1859年A.凱萊將拉蓋爾思想進一步發揮，得到角的射影測度的概念。首先，將拉蓋爾公式中的一對圓點,看作是變態(退化)的二級曲線,並以常態（非退化）二級曲線來代替。於是作了如下的推廣：在射影平面內，先選定一個常態二級曲線及一個任意常數 k(k≠0),再過任意給定的兩條直線α與b的交點,作二級曲線的兩條切線t1與t2，並規定了一個函式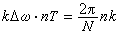(α,b；t1,t2)，顯然這個函式對任意給定的兩直線α,b,其交點α×b及過交點的兩條切線t1，t2都是確定的,從而kln(α,b;t1,t2)除了一個符號外,也被確定。而且函式φ(α,b)滿足以下條件: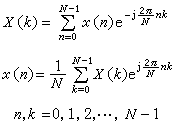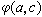，這裡α、b、с 是共點的三條直線。 而這些條件正是歐氏幾何中二條直線所成角度應當滿足的，因此將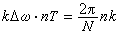 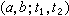叫做兩直線α，b所成角的射影測度,預先取定的二級曲線叫做這個測度的絕對形，而k叫做測度係數。
有了角的射影測度，可對偶地建立另一種形式的測度：取定一條常態二階曲線及一個非零的任意常數k,連結任意給定的兩點A,B,設直線A×B與二階曲線交於兩點T1及T2，且規定函式d(A,B)=kln（A,B;T1;T2）,顯然它是A,B的函式,且滿足歐氏幾何中兩點間有向距離的條件：d(A,A)=0,d(B,A)=-d(A,B),d(A,B)+d(B,C)=d(A,C),這裡A,B,C是共線的三點。因此將函式d(A,B)=kln(A,B;T1,T2)，叫做A,B兩點間的有向距離，因為它是利用射影概念交比定義的，所以又叫做距離的射影測度。預先給定的二階曲線叫做測度的絕對形,k叫做測度係數。若已知常態二階曲線的方程是

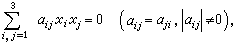
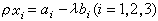二已知點A,B的坐標分別是(α1,α2,α3),b1,b2,b3,A、B聯線上任意一點的坐標可寫作將其代入二階曲線方程中,得到關於λ的一個二次方程,它的兩個根分別以λ1及λ2表示，則T 1及T 2的坐標為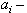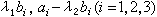,再利用交比的性質：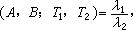

可得到d(A,B)的解析表達式。關於φ(α,b的解析表達式可利用完全相同的方法得出。上面以二次曲線（二階與二級）為絕對形,規定了射影測度的概念。應該指出,確定距離的射影測度的絕對形即常態二階曲線，其切線的集合構成了用以確定角的射影測度的絕對形即常態二級曲線。由於二次曲線有實虛之分，取實虛不同的二次曲線作絕對形，這樣就構成了與歐氏幾何完全不同的非歐幾何（羅氏幾何和黎曼幾何）的模型（見非歐幾里得幾何學）。1871年F.克萊因首先發明使用射影測度來說明非歐幾何。簡單來說，他在復射影平面上的實絕對形內部，規定了一些具體概念，定義射影測度後，作成了一個羅氏幾何的射影模型即克萊因模型,在這個模型里,羅氏幾何的全部公理都能夠得到解釋，因而羅氏幾何的全部概念和定理都能在模型中體現出來。
參考書目
　孫澤瀛編：《近世幾何學》，高等教育出版社，北京，1959。

配圖

相關連線