大系統的分解和協調
正文
將大系統分解成若干相對獨立的子系統並用協調器來處理各子系統間的關聯作用的一種遞階控制方法。通常將大系統分解成若干個相對獨立而又相互關聯的子系統作為第一級（下級系統），分別求解每個子系統的極值問題，並在第二次(上級系統)設定一個協調機構（協調器）來處理各子系統間的關聯作用。通過上下級之間反覆交換信息，在求得各子系統極值解的同時，獲得整個大系統的最優解。在遞階系統中，分解和協調是密切相關的兩個基本過程。在分解過程中,可以按三種觀點來劃分子系統:①基於實際系統結構的分解;②基於計算量最小的分解;③基於決策問題數學結構的分解。但無論是哪一種分解，都應使每個子系統在協調器提供協調變數值的情況下，獨立地求解各自的極值問題。為此，一方面將大系統的總體目標以適當的形式分配給每個子系統，另一方面在保持整體最優解不變的前提下，對每個子系統中的關聯項作某些調整。
協調過程是一個對總體目標尋優的過程。上級系統憑藉它所能支配的協調變數去命令下級系統，使下級各子系統的動作協調起來，以便在求得各下級子系統的局部極值解的同時，獲得大系統的整體最優解。既然協調器的任務在於從總體目標出發，溝通並處理下級各子系統間的關聯，那么就有一個依據何種原理和採用什麼策略有效地調配下級系統的問題。歸根到底是選擇哪個變數作為協調變數的問題。為使協調能達到預期的目的，還要引入可協調性的概念。一個系統按某個原理是可協調的，是指該原理為可行的，並存在一個協調變數，使相應的協調條件得到滿足。
對於線性二次型問題，可線上性狀態方程和線性關聯方程的約束下求二次型目標函式J的極小解。根據拉格朗日乘子理論，這一問題可化成無約束極值問題。即求拉格朗日函式
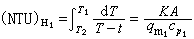的極小解,求L的極小解相當於求每個子系統的拉格朗日函式Li的極小解。按照拉格朗日對偶理論，可把一個求有約束的問題的極小解，變換成一個求無約束的對偶問題的極大極小解。即定義一個拉格朗日對偶函式
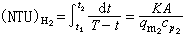，在滿足一組凸性條件下使下式成立：
。這就是大系統分解協調的理論依據。這裡ρ是拉格朗日乘子，λ是關聯拉格朗日乘子，x是狀態變數，u是控制變數，z是關聯輸入變數。選擇不同的協調變數,可以構成各種不同的遞階控制方法。其中最基本的是目標協調法、模型協調法和混合法。 目標協調法 選擇關聯拉格朗日乘子λ作為協調變數來求解下列極值問題的兩級遞階算法：
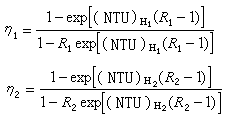
模型協調法 選擇輸出變數 y作為協調變數來求下列極值問題的一種兩級遞階算法：
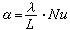
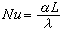（式中zi是第i個子系統的關聯輸入變數, Mij是常數矩陣,yj是第j個子系統的輸出變數），所有中間結果都是物理上可實現的，因此這種算法也叫可行分解法。 因為直接選擇輸出變數y作為協調變數,故又稱直接法。 混合法 這是選擇關聯拉格朗日乘子λ和關聯輸入變數z 作為協調變數來求下列極值問題的一種兩級遞階算法：
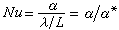
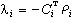和
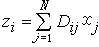（式中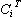
是轉置矩陣, Dij是常數矩陣）按預定的精度同時滿足為止。 由於這種算法把關聯拉格朗日乘子λ和關聯輸入變數 z兩者作為協調變數，它本質上是目標協調法和模型協調法的綜合,因而稱為混合法。鑒於每次疊代都要對關聯輸入變數z 進行預估，所以也叫關聯預估法。 參考書目
M.D.Mesarovic et al.， Theory of Hierarchical Multilevel Systems, Academic Press, New York, 1970.
M.G.辛，A.鐵脫里編著，周斌等譯：《大系統的最最佳化及控制》,機械工業出版社，北京,1983。(M.G.Singhand A.Titli, Systems：Decomposition，Optimization and Control, Pergamon Press, Oxford,1978.)
