基本介紹
設V是域P上n維線性空間,且ε,ε,…,ε與ε′,ε′,…,ε′皆是V的基,於是有:
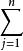 坐標變換公式
坐標變換公式ε′= aε(i=1,2,…,n).
以ε′關於基ε,ε,…,ε的坐標(a,a,…,a)為第i列構成的n階矩陣(a)稱為由基ε,ε,…,ε到基ε′,ε′,…,ε′的過渡矩陣,若α∈V關於基ε,ε,…,ε與基ε′,ε′,…,ε′的坐標分別為(x,x,…,x)與(x′,x′,…,x′),則其兩坐標間的關係,可由過渡矩陣(a)表示為
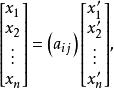 坐標變換公式
坐標變換公式上式稱為坐標變換公式 。
坐標變換公式的證明
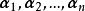 坐標變換公式
坐標變換公式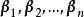 坐標變換公式
坐標變換公式設和是線性空間V中的兩個基,並且
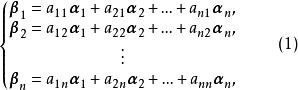 坐標變換公式
坐標變換公式式(1)可表示為
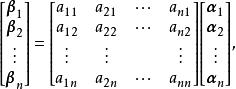 坐標變換公式
坐標變換公式即
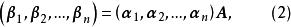 坐標變換公式
坐標變換公式其中
 坐標變換公式
坐標變換公式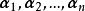 坐標變換公式
坐標變換公式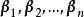 坐標變換公式
坐標變換公式((2)式中A應為A的轉置)式(1)或式(2)稱為基變換公式,矩陣 A稱為由基到基的過渡矩陣。
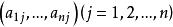 坐標變換公式
坐標變換公式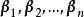 坐標變換公式
坐標變換公式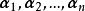 坐標變換公式
坐標變換公式注意:式(1)中各式的係數實際上是基向量在基下的坐標 。
坐標變換公式及其證明:
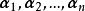 坐標變換公式
坐標變換公式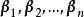 坐標變換公式
坐標變換公式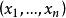 坐標變換公式
坐標變換公式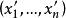 坐標變換公式
坐標變換公式定理1設V中一向量ξ在兩個基和下的坐標分別是和,若兩個基滿足關係式(2) ,則有坐標變換公式:
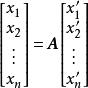 坐標變換公式
坐標變換公式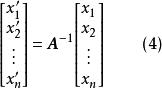 坐標變換公式
坐標變換公式或
 坐標變換公式
坐標變換公式證明:因為
 坐標變換公式
坐標變換公式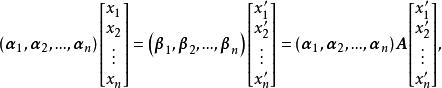 坐標變換公式
坐標變換公式故由坐標的唯一性,得
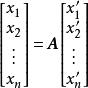 坐標變換公式
坐標變換公式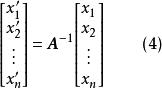 坐標變換公式
坐標變換公式或
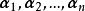 坐標變換公式
坐標變換公式反之,設是線性空間V的一個基,A是n階可逆矩陣,使得
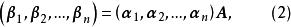 坐標變換公式
坐標變換公式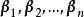 坐標變換公式
坐標變換公式成立,可以證明:是V的n個線性無關的向量,從而也是V的一個基 。
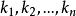 坐標變換公式
坐標變換公式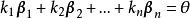 坐標變換公式
坐標變換公式證明若數使,
即
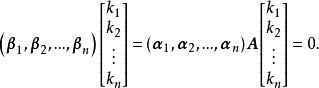 坐標變換公式
坐標變換公式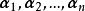 坐標變換公式
坐標變換公式因為線性無關,故必有
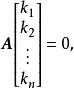 坐標變換公式
坐標變換公式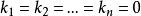 坐標變換公式
坐標變換公式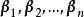 坐標變換公式
坐標變換公式但 A可逆,即| A|≠0,齊次線性方程組 AX= 0只有零解,必有,線性無關 。